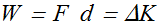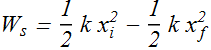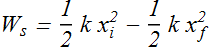Work and Kinetic Energy
Objectives
In this chapter we will learn the following concepts:
Energy is a scalar quantity.
Energy is conserved: The change in energy of a system plus the change in energy of surroundings is zero.
A single particle is the simplest possible system.
Single particle energy has two parts:
Rest energy (energy an object has even when at rest)
Kinetic energy (energy associated with motion)
The energy of the system can be changed only by external forces.
Work is energy transfer into or out of a system.
Work involves external force acting through a distance.
Work can be positive or negative.
Computation of work due to a variable force.
Work done by a spring force.
Power is the time rate of energy transfer into or out of a system
The Energy Principle
In everyday life we see flow of energy in our daily life.
We ingest chemical energy in the form of food and use this energy in our activities.
We put chemical energy in the form of gasoline into our car, and car uses up this energy to run the engine.
You compress a spring, and the mechanical energy stored in the spring can launch a ball.
Conservation of energy
Energy can neither be created nor be destroyed, but it can change form. The only way for system to gain or loose energy is if the surroundings loose or gain the same amount of energy.
![]()
ΔE is a change in energy, which is final energy minus initial energy,
![]()
The energy principle is fundamental principle.
The validity of the energy principle has been verified through a wide variety of observations and experiments.
A Single Particle (The Simplest System)
The simplest particle system consists of a single particle.
"A particle" could be a proton or an electron, a baseball or even a planet.
According to Einstein the energy ![]() of a particle moving with speed v is given by the expression:
of a particle moving with speed v is given by the expression:
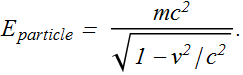
The unit of energy is joule, abbreviated "J".
![]()
![]() is the speed of light.
is the speed of light.
What is energy?
When a particle is at rest, what is its energy?
When a particle is at rest, its speed v=0, therefore
![]()
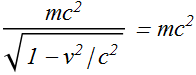
That means when the particle is at rest, its energy is given as
![]()
We call ![]() the "rest energy" of a particle at rest.
the "rest energy" of a particle at rest.
Einstein realized that the mass of an object is its energy content divided by a constant: ![]() .
.
In real sense, mass and energy
is same thing, although for historical reasons we use different units for them: mass in Kg and energy in joules.
For example a hot object, with more thermal energy, has slightly more mass than a cold object.
Kinetic Energy
Let us plot energy of a particle in the units of its "rest energy" as a function of v/c.
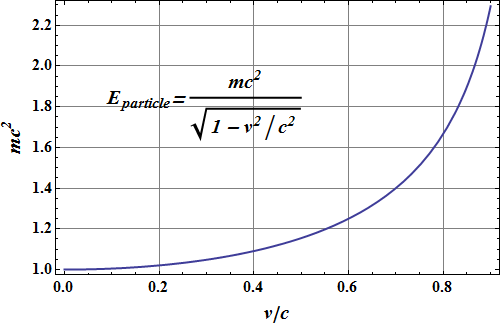
We can see that energy of the particle increases with increase in speed.
As consequence of its motion, the particle has additional energy, known as "kinetic Energy" K.
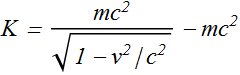
The kinetic energy K of a particle is the energy, a moving particle has in addition to its rest energy.
Let us use the "binomial expansion" and we get the expression of the energy as
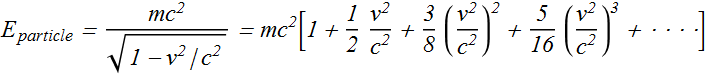
Or
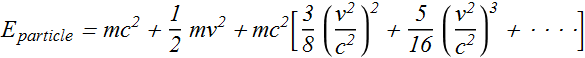
It can be seen that energy of a particle can be written as
![]()
Where the expression for Kinetic Energy K can be written as
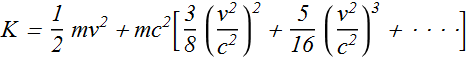
Example 1: Energy of a fast moving proton
A proton in a particle accelerator has a speed of ![]() .(a) What is the energy of the proton? (b) What would the energy of the proton be if it were
sitting still? (c) What is the kinetic energy of the moving proton?
.(a) What is the energy of the proton? (b) What would the energy of the proton be if it were
sitting still? (c) What is the kinetic energy of the moving proton? ![]() .
.
Kinetic Energy at Low - Speed
Let us consider a particle moving with a speed v that is much small compared to the speed of light (v<<c).
As we have seen with "binomial expansion", the expression for the kinetic energy K of a particle can be written as
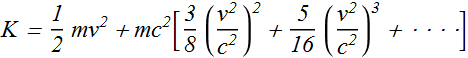
When v<<c, then v/c << 1, therefore higher powers of v/c will be further small and can be neglected.
We can say that at (v<<c) Low-Speed Kinetic Energy can be given as
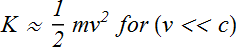
Since we will be dealing with low speed (v<<c) problems, therefore whenever we use the term kinetic energy, we mean approximate kinetic energy.
Example 2: Kinetic Energy of a fast moving proton with approximate formula
Calculate the Kinetic energy of the proton in a particle accelerator given in example 1 with approximate formula. Proton speed was ![]() .
. ![]() .
.
Example 3: Approximate Kinetic Energy
The solar wind consists of charged particles streaming away from sun. The speed of a proton in the solar wind can be as high as ![]() . What is the kinetic energy of such a proton?
. What is the kinetic energy of such a proton? ![]() .
.
Is it appropriate to use approximate formula for Kinetic Energy in this case?
Work
Work is defined as energy transferred into or from a system.
Consider a bead of mass m moving with initial velocity ![]() along a frictionless wire.
along a frictionless wire.
What is its (initial) kinetic energy?
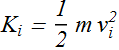
On the way, (Click Play to move) we apply force ![]() , directed at an angle φ to the wire. After a displacement
, directed at an angle φ to the wire. After a displacement ![]() along x-axis the velocity of bead has changed to
along x-axis the velocity of bead has changed to ![]() .
.
Now what is its (final) kinetic energy?
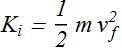
How much energy is transferred to the bead? Or how much is the change in energy of bead?
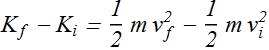
As per definition of work this change in energy of the bead, produced by the applied force is called work W.
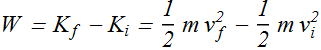
Mathematically we can write it as
![]()
This is also known as work-kinetic energy theorem.
Relation between work and applied force.
If force is a constant (constant acceleration) according to kinematic equation the final velocity ![]() is related to displacement
is related to displacement ![]() and acceleration along x-axis (direction of motion).
and acceleration along x-axis (direction of motion).
![]()
Multiply both sides by ![]() .
.
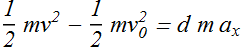
As per above equation change in kinetic energy can be given as
![]()
Or work is related to the displacement and acceleration as
![]()
Which component of force will cause the change in magnitude of bead velocity?
As per Newton's law, the product ![]() is nothing but the x-component
is nothing but the x-component ![]() of the applied force
of the applied force ![]() .
.
![]()
By substituting ![]() we get
we get
![]()
Term d F cos φ is the dot product ![]() of displacement
of displacement ![]() and applied force
and applied force ![]() , therefore we can write work W as
, therefore we can write work W as
![]()
The SI unit of Work is Joule (J) same as units of energy.
![]()
Work W is energy transferred to or from an object by means of a force acting on the object.
Energy transferred to the object is positive work.
Energy transferred from the object is negative work.
Although this expression is derived from change in energy of a single particle but for any force acting on a system, work W is defined as the dot product ![]() of the force
of the force ![]() and the displacement
and the displacement ![]() caused by that force. Since dot product of two vectors is a scalar, therefore work W is a scalar quantity.
caused by that force. Since dot product of two vectors is a scalar, therefore work W is a scalar quantity.
Checkpoint - 1
A particle moves along an axis. Does the kinetic energy of the particle increase, decrease, or remain the same if the particle’s velocity changes
(a) from −3 m/s to −2 m/s and
(b) from −2 m/s to 2 m/s?
(c) In each situation, is the work done on the particle positive, negative, or zero?
Example 4: Work
A paper airplane flies from location ![]() to location
to location ![]() .
.
The net force acting on it during this flight, due to the earth and the air, is nearly constant at ![]() .
.
What is the total work done on the paper airplane by the earth and the air?
Example 5: Work
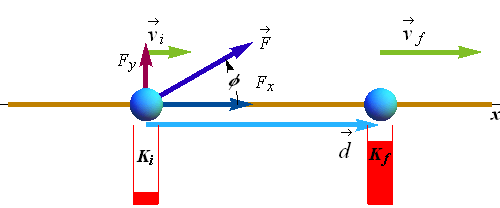
A coin slides over a frictionless plane and across an xy coordinate system from the origin to a point with x y coordinates (3.0 m, 4.0 m) while a constant force acts on it. The force has magnitude 2.0 N and is directed at a counterclockwise angle of 100° from the positive direction of the x axis.
How much work is done by the force on the coin during the displacement?
Example 6: Work and Kinetic Energy
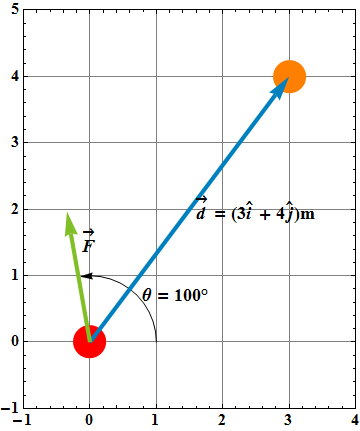
An 8.0 kg object is moving in the positive direction of x axis. When it passes through x=0 m, a constant force directed along the axis begins to act on it. Following figure gives its kinetic energy K versus position x as it moves from
x = 0 m to
x = 5 m ; ![]() . The force continues to act.
. The force continues to act.
What is v when the object moves back through
x = -3 m?
Work Done by the Gravitational Force
Consider a bouncing ball (click play to throw ) of mass m that is thrown upward from point, with initial speed ![]() .
.
What is its initial kinetic energy ?
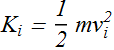
As the ball rises, its speed v (red arrow) reduces, that means, the ball’s kinetic energy decreases to?
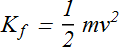
Which force is responsible for decreasing the kinetic energy of ball?
Gravitational force ![]() .
.
Gravitation force is doing a negative work ![]() when the ball is moving up with positive displacement
when the ball is moving up with positive displacement ![]() .
.
The work ![]() done by the gravitational force on the ball for upward displacement
done by the gravitational force on the ball for upward displacement ![]() is:
is:
![]()
Minus sign means gravitational force takes away energy from the object when it moves up.
What will be the work done ![]() by gravitational force
by gravitational force ![]() when ball moves down?
when ball moves down?
When ball moves downward, the angle between ![]() and downward displacement
and downward displacement ![]() is 0°, the work
is 0°, the work ![]() done by the gravitational is:
done by the gravitational is:
![]()
Plus sign means gravitational force gives energy back to the object when it moves down.
Checkpoint - 2
A ball is moving upwards, acted on by a downwards gravitational force.
Is the kinetic energy of the ball increasing or decreasing?
Is the work done by the gravitational force positive or negative?
Checkpoint - 3
A greased pig has a choice of three frictionless slides along which to slide to the ground. Rank the slides according to how much work the gravitational force does on the pig during the descent, greatest first.
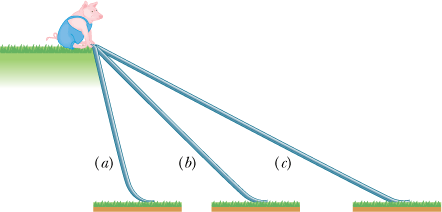
How to compute Work if force is Variable?
Work done by a constant force is given as the product of displacement and the component of the force along the displacement.
What about variable force?
Consider a variable force acting on an object along x-axis.
Work done along x-axis, needs only x-component of force F(x).
Plot the magnitude of x-component of force F(x) as a function of position x.
Let us calculate the work W that F does on an object to move it from ![]() to
to ![]() .
.
First divide the interval ![]() into N “elements” of length Δx (select Show) such that we can assume that force is constant for each small displacement Δx.
into N “elements” of length Δx (select Show) such that we can assume that force is constant for each small displacement Δx.
Since force is assumed to be constant in the interval Δx
therefore if ![]() is the average force in the 4th interval, the work done
is the average force in the 4th interval, the work done ![]() in 4th interval is
in 4th interval is
![]()
Now the total work done can be computed by adding work done over all the intervals.
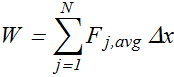
From knowledge of calculus we know if we take limit N→∞ or Δx→0, we get
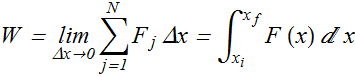
We can see for very small value of Δx (take Δx slider to minimum) , geometrically, W is area of the curve from ![]() to
to ![]() .
.
Checkpoint - 4
Following figure gives the x component ![]() of a force that can act on a particle. If the particle begins at x = 0, with some initial kinetic energy, what is its coordinate when it has
of a force that can act on a particle. If the particle begins at x = 0, with some initial kinetic energy, what is its coordinate when it has
(a)
maximum kinetic energy and (b) maximum speed?
(c) How much work is done by the force, by the time particle reaches
x = 6 m?
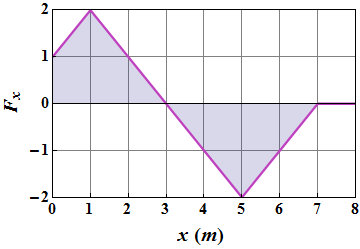
Example of variable Force
Spring Force
Spring force is an example of variable force.
When we pull (click-hold and drag the block to right) one end of the spring and stretch it by amount ![]() .
.
Spring resists by exerting a force ![]() in opposite direction.
in opposite direction.
When we push (click-hold and drag the block to left) one end of the spring and compress it by amount ![]() .
.
Again the spring resists by exerting a force ![]() in opposite direction.
in opposite direction.
This force is called spring force or restoring force, and is given as
![]()
This is also known as Hook's law and k is called spring's constant.
In one dimension we can write it as
![]()
Work done by a Spring Force
Spring force is a variable force, work done by any variable force in one dimension is given as
In one dimension spring force is written as
![]()
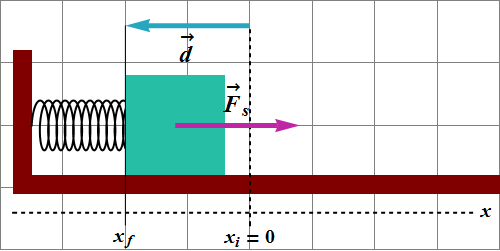
If spring moves from ![]() to
to ![]() , work
, work ![]() done by spring force can be computed as
done by spring force can be computed as
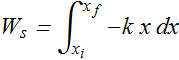
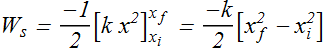
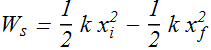
If initial position ![]() (equilibrium), work
(equilibrium), work ![]() done by spring force can written as
done by spring force can written as
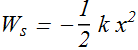
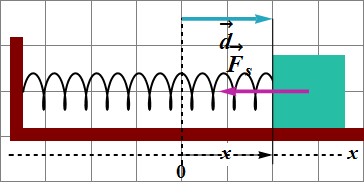
Example 7: Work Done by Spring Force
Fig. 1 gives spring force versus position x for the spring–block arrangement of Fig. 2. After pulling,
the block was released from x = 12 cm.
How much work does the spring do on the block when the block moves from x = 8.0 cm to (a)
x = 5.0 cm, (b) x = -8.0 cm?
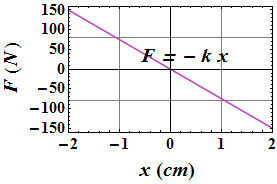 |
 |
| Fig. 1 | Fig. 2 |
Power
The time rate of energy transfer into or out of a system is called power.
If change in kinetic energy ΔK of a system takes place in time Δt, the average power ![]() is defined as
is defined as
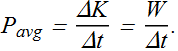
The instantaneous power P is the instantaneous time rate of change of energy
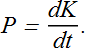
The SI unit of power is the joule per second. This unit is called watt (W).
![]()
Power is a scalar quantity
A commonly used non SI unit is horsepower
The kilowatt-hour (k Wh) is a unit of work (power multiplied by time). It is used by electrical utility companies.
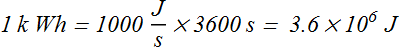
Instantaneous power and Velocity
If the work is done by a force ![]() through a displacement of
through a displacement of ![]() , the average power can be written as
, the average power can be written as
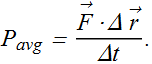
If the work is done by a constant force, average power will be
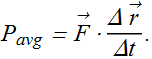
The instantaneous power can now be given as
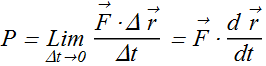
Here 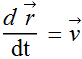 is the instantaneous velocity of the object.
is the instantaneous velocity of the object.
Therefore if force is constant, instantaneous power can be given as
![]()
Checkpoint 3
A block moves with uniform circular motion because a cord tied to the block is anchored at the center of a circle. Is the power due to the force on the block from the cord positive, negative, or zero?
Example 8: Power
The loaded cab of an elevator has a mass of ![]() and moves
210 m up the shaft in 23 s at constant speed.
and moves
210 m up the shaft in 23 s at constant speed.
At what average rate does the
force from the cable do work on the cab?