Waves-II
Objectives
In this chapter we will cover sound waves and by the end after finishing the chapter we should know following topics:
Speed of sound waves
Relation between displacement and pressure amplitude
Sound intensity and sound level
What are Sound Waves?
Sound waves are mechanical longitudinal waves that propagate in solids, liquids and gases.
Seismic waves used by oil explorers propagate in the earth’s crust.
Sound waves generated by a sonar system propagate in the sea.
An orchestra creates sound waves that propagate in the air.
When a tiny sound source (we can call it a point source) generates sound, the sound waves propagate like expanding spheres.
Surface of these expanding spheres is called wave front.
A cross section of this wave propagation is shown in the simulation.
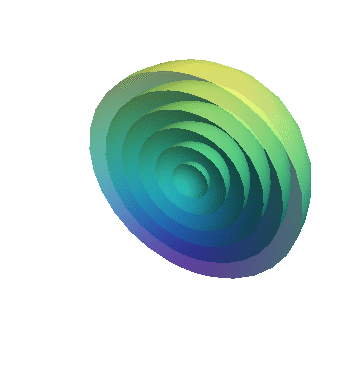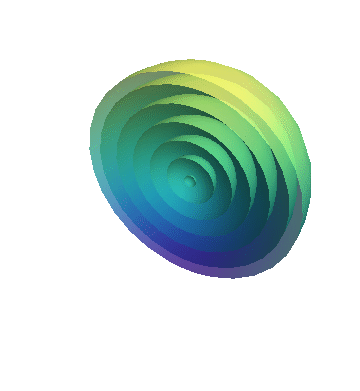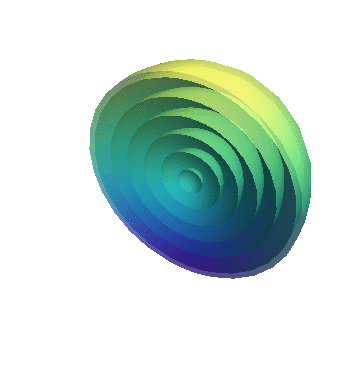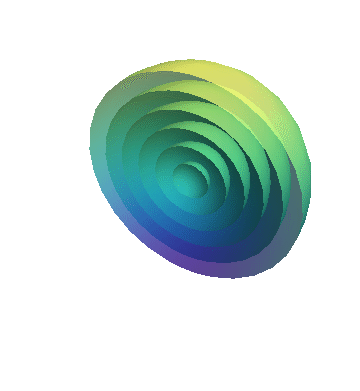
Propagating sound waves on the surface of water (cross section of the sphere) are shown in the following simulation.

Travelling Sound Waves
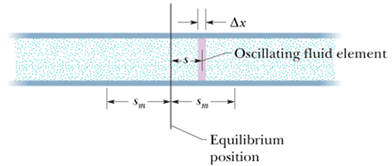
Consider a tube filled with air molecules. A piston attached on one end oscillate (Click play) to produce sound wave.
As the wave passes, air columns oscillates about their equilibrium positions (watch the motion of green columns).
The maximum displacement ![]() of each element is either left or right.
of each element is either left or right.

We can see that, the variation of displacement produces places of compression and rarefaction in the air column.
This produces variation of pressure at different locations in the column. The pressure in the column can be written as
![]()
Here ![]() is pressure amplitude, which is the maximum increase or decrease in pressure.
is pressure amplitude, which is the maximum increase or decrease in pressure.
Checkpoint-1: (Traveling Sound Wave)
When the oscillating air element in the figure is moving rightward through the point of zero displacement, is the pressure in the element at its equilibrium value, just beginning to increase, or just beginning to decrease?
The Speed of Sound
As we have seen, sound waves produce change in pressure Δp.
When we apply pressure Δp on an object of volume V, it results in the change of volume ΔV.
The bulk modulus B of a medium relates change in pressure and fractional change in volume.
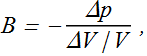
Negative sign indicates decrease in volume when Δp is positive.
The speed v of sound in such a medium is given by
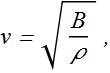
Where ρ is volume density of the medium.
Bulk modulus B is smaller for more compressible mediums. Such mediums will exhibit lower speed of sound.
Mediums with higher density will also exhibit lower speed of sound.
Intensity and sound Wave
The intensity I of a sound wave at a surface is the average rate per unit area at which energy is transferred by the wave.
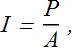
Where P is the power (rate of energy transfer) of sound wave and A is the area of the surface intercepting the sound.
Intensity I of the sound at a location is related to the amplitude ![]() of the wave.
of the wave.
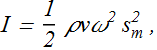
Consider a sphere of radius r enclosing a sound producing point source at the center of the sphere.
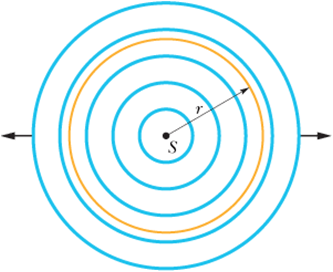
If P is the rate of energy emitted by the source, then the intensity of sound on the walls of the sphere will be
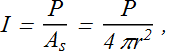
We can see that as we increase the radius of the sphere the intensity of the sound decreases by the square of radius r.
This means as we go away from the source of a sound the intensity of the sound reduces by square of the distance r from the source.
Checkpoint-2: (Intensity of Sound)
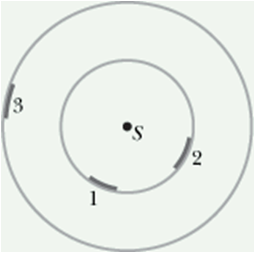
The figure indicates three small patches 1, 2, and 3 that lie on the surfaces of two imaginary spheres; the spheres are centered on an isotropic point source S of sound. The rates at which energy is transmitted through the three patches by the sound waves are equal.
Rank the patches according to (a) the intensity of the sound on them and (b) their area, greatest first.
The Decibel Scale
The displacement amplitude at the human ear ranges from about ![]() for the loudest tolerable sound to about
for the loudest tolerable sound to about ![]() m for the faintest detectable sound, a ratio of
m for the faintest detectable sound, a ratio of ![]() .
.
We deal with such an enormous range of values by using logarithms. Consider the relation
![]()
It is a property of this equation that if we multiply x by 10, then y increases by 1.
![]()
Similarly, if we multiply x by ![]() , y increases by only 12.
, y increases by only 12.
Thus, instead of speaking of the intensity I of a sound wave, it is much more convenient to speak of its sound level β, defined as
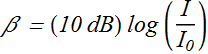
Here dB is the abbreviation for decibel, the unit of sound level, (the name was chosen to recognize the work of Alexander Graham Bell)
![]() is standard reference intensity
is standard reference intensity ![]() ). It is near the lower limit of human range of listening.
). It is near the lower limit of human range of listening.
Standing Sound Waves
Like any other waves, interference of two sound waves travelling in opposite direction will produce standing waves.
Since sound waves produce pressure waves given by
![]()
The resulting standing wave will produce regions of high pressure points (anti-nodes) and anti-pressure points (nodes).
Sound can cause the wall of a drinking glass to oscillate. If the standing waves are produced with large enough intensity, the glass will shatter.
