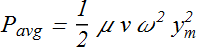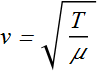Waves-I
Objectives
In this chapter we will introduce the concept of waves and after finishing the chapter we should know following topics:
Types of waves
Amplitude, phase, frequency, period, wave number and wavelength.
Speed of a wave
Superposition of waves
Wave interference
Standing waves, resonance
Mechanical waves propagating along a stretched string
What are Waves?
Whenever we hear any sound produced by a source.
The source generates waves (sound waves) and we detect it with our ears.
There are three main types of waves:
Mechanical Waves:
Water waves, sound waves and seismic waves.
They are governed by Newton's laws, and they can exist only within a material medium, such as water, air, and rock.
Electromagnetic waves:
Visible and ultraviolet light, radio and television waves, microwaves, x rays, and radar waves.
These waves require no material medium to exist.
All electromagnetic waves travel through vacuum at the same speed c = 299792458 m/s.
Matter waves:
These waves are associated with electrons, protons, and other fundamental particles, and even atoms and molecules.
These particles are considered as constituting matter, such waves are called matter waves.
Transverse Waves
A wave sent along a stretched, taut string (here we are using a string made of beads and thread) is an example of transverse mechanical wave.
Generate a single pulse on the string (Click Play).
Generate a sinusoidal wave on the string (Click Play).
In Transverse waves the displacement of every oscillating element (bead) is perpendicular to the direction of travel of the wave. (focus on the motion of green beads)
Longitudinal Waves
Consider a tube filled with air molecules. A piston attached on one end oscillate (Click play) to produce sound wave.
This is an example of longitudinal mechanical wave.
Focus on the motion of green particles; it is just oscillating parallel to the direction of motion around their equilibrium positions at 1, 3 and 5.
In longitudinal waves, the motion of the atom/molecules of the medium (air, water etc.) is parallel to the direction of the wave.
Both a transverse waves and a longitudinal waves are said to be traveling waves because they both travel from one point to another
Function Describing a Wave
To completely describe a wave on a string we need a function that gives the shape of the wave.
For a sinusoidal wave traveling in the positive direction of x-axis, the displacement y(x, t) (transverse or longitudinal) of any string element at position x and at time t, can be written as.
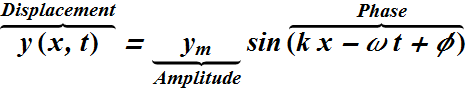
Different constant in phase term (k x-ω t +φ) as follow
k is Angular wave number.
ω is angular frequency.
φ is initial phase or phase constant.
Angular frequency, Frequency & Period
If we plot the displacement of single element (bead) on the string at x = 0, the displacement y(0, t) of the element must return to its initial value after one time period T.
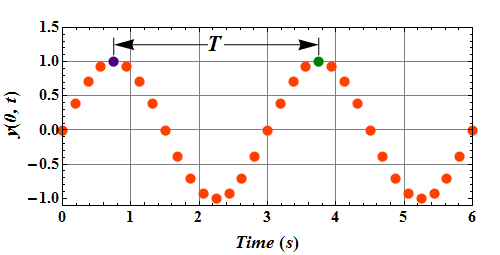
![]()
![]()
![]()
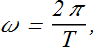
Frequency f of the wave is related to its angular frequency.
![]()
Wavelength & Angular Wave Number
Wavelength λ is another quantity associated with any wave and it is related to the wave number k.
The wavelength λ of a wave is the distance between repetitions of the shape of the wave (or wave shape). In a snapshot of the wave at time t = 0, the displacement of an element at x should be same as of an element at x+λ
![]()
![]()
![]()
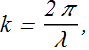
The wavelength λ of a wave is the distance between repetitions of the shape of the wave (or wave shape).
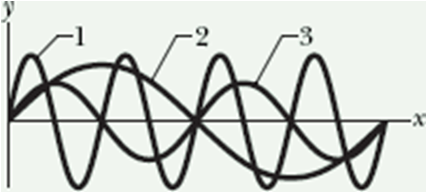
Checkpoint-1: (Wavelength and Frequency)
The figure is a composite of three snapshots, each of a wave traveling along a particular string. The phases for the waves are given by (a)
2x-4t, (b) 4x-8t, and (c) 8x-16t.
Which phase corresponds to which wave in the figure?
Phase Constant (Initial phase)
When the amplitude and slope of a wave at x = 0 and t = 0 is not zero, a constant phase φ can be inserted in the wave equation to describe its initial amplitude.
![]()
How to calculate constant Phase for a given wave?
Velocity of the oscillating particle at a position x is given as
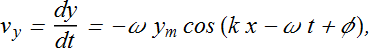
For a given value of x and t the ratio of ![]() is given as
is given as
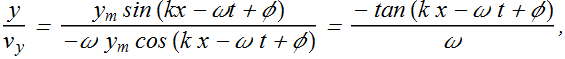
If velocity of a particle and its amplitude at a given time and position is know we can find the value of constant phase φ for that wave.
Consider a wave with angular frequency ω = 5 rad/s. If at t = 0 and x = 0, ![]() and y = 2.0 cm the phase constant can be computed as
and y = 2.0 cm the phase constant can be computed as
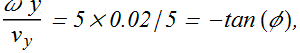
![]()
Checkpoint-2: (Wavelength and Frequency)
At time t = 0 the point at x = 0 of a string carrying a traveling sinusoidal wave has a velocity of 0 and a positive displacement.
What is the value of the phase constant φ?
![]()
Speed of a Traveling Wave
Following is the snapshot of a wave at time t. Let the wave move for Δt time (click play) and take another snapshot at time t+Δt.
Suppose the entire wave pattern moves a distance Δx in positive x direction during the time interval Δt.
The wave speed v is given as

How can we find value of wave speed v?
The displacement ![]() of purple particle (1st snapshot) at position x and at time t is given as
of purple particle (1st snapshot) at position x and at time t is given as
![]()
The displacement ![]() of green particle (2nd snapshot) at position x+Δx and time t = t + Δt is given as
of green particle (2nd snapshot) at position x+Δx and time t = t + Δt is given as
![]()
We can see in the picture, the displacement of purple particle in 1st snapshot is equal to displacement of green particle in 2nd snapshot.
![]()
This is only possible when the phases of two particles are equal, in other words
![]()
![]()
Above relation is true for any particle. When a term k Δx is added to the phase, an equal term ω Δt is subtracted. This implies that the phase (k x-ω t) of a wave always remains constant.
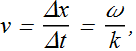
In terms of wavelength λ and frequency f, the speed of a wave can be written as
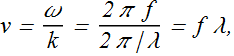
Direction of traveling wave?
We have seen that the value of v=ω/k is positive for a wave ![]() .
.
Thus a wave with phase value (k x-ω t) always moves along positive x direction.
While a wave ![]() will always travel in negative x direction.
will always travel in negative x direction.
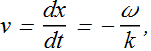
Consider now an arbitrary function h of phase term k x±ω t
![]()
This function represents a traveling wave. Thus we can say that any arbitrary function of phase k x±ω t, represents a traveling wave.
The speed of such a wave is given as v=∓ω/k .
Checkpoint-3: (Speed of a wave)
Here are the equations of three waves: (1) y(x,t)=2sin(4x-2t), (2) y(x,t)=sin(3x-4t), (3) y(x,t)=2sin(3x-3t).
Rank the waves according to their wave speed, greatest first.
Checkpoint-4: (wave function)
Among the following two function, which function represent a wave?
(1) ![]() , (2)
, (2) ![]() ,
,
The principle of superposition for waves
Often two or more waves pass simultaneously through a medium. When we listen to a concert, for example, sound waves from many instruments fall simultaneously on our eardrums.
Suppose that two waves with displacement ![]() and
and ![]() , travel simultaneously along the same stretched string.
, travel simultaneously along the same stretched string.
Displacement ![]() of string due to these two waves is given as
of string due to these two waves is given as
![]()
Overlapping waves algebraically add to produce a resultant wave (or net wave).
Overlapping waves do not in any way alter the frequency of each other.
Interference of waves
Let us consider that two sinusoidal waves ![]() and
and ![]() of the same wavelength and amplitude, traveling in the same direction along a stretched string.
of the same wavelength and amplitude, traveling in the same direction along a stretched string.
![]()
![]()
φ is the phase difference between the two waves.
What resultant wave does it predict for the string?
Net displacement of string ![]() will follow principle of superposition
will follow principle of superposition
![]()
As per trigonometric relation
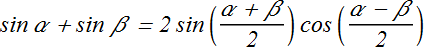
Therefore

This phenomenon of combining waves is called interference.
The resultant amplitude of resulting wave depends on the phase difference φ between the two waves
Terms Used in a two interfering waves
The resultant wave due to the interference of two sinusoidal transverse waves, is also a sinusoidal transverse wave, with an amplitude and an oscillating term.

The quantity 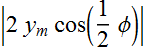 can be viewed as the amplitude of the net wave on the string.
can be viewed as the amplitude of the net wave on the string.
The quantity sin(k x-ω t+φ/2) is the oscillating term and has same angular frequency.
Interference when φ=0
If φ = 0 rad (or 0°), the two interfering waves (orange and green) are exactly in phase. The value of
![]()
Therefore
![]()
The amplitude of the resultant wave (blue) is twice the amplitude of either interfering wave. That is the greatest amplitude the resultant wave can have.
Interference that produces the greatest possible amplitude is called fully constructive interference.
Interference when φ=π
If φ=π rad (or 180°), the two interfering waves (orange and green) are opposite in phase. The value of
![]()
Therefore
![]()
The amplitude of the resultant wave (blue) is zero for all values of x and t.
Although two waves are present on the string, we see no motion of the string.
This type of interference is called fully destructive interference.
Interference when φ=2π/3
If φ=2π/3 Read (or 120°), the two interfering waves (orange and green) are in intermediate phase. The value of
![]()
Therefore
![]()
The amplitude of the resultant wave (blue) is equal to the amplitude of either interfering wave (orange and green).
When interference is neither fully constructive nor fully destructive, it is called intermediate interference.
Interference when φ=3π/2
If φ=3π/2 rad (or 270°), the two interfering waves (orange and green) are in intermediate phase. The value of
![]()
Therefore
![]()
The amplitude of the resultant wave (blue) is equal to the amplitude of either interfering wave (orange and green).
When interference is neither fully constructive nor fully destructive, it is called intermediate interference.
Checkpoint-5: (Interference)
Here are four possible phase differences between two identical waves, expressed in wavelengths: 0.20, 0.45, 0.60, and 0.80.
Rank them according to the amplitude of the resultant wave, greatest first.
Key Idea: Φ = 0.20 wavelength means Φ = 0.20 (2 π)
Problem-2: (Interference)
Two identical sinusoidal waves, moving in the same direction along a stretched string, interfere with each other. The amplitude ![]() of each wave is 9.8 mm, and the phase difference between them is 85°.
of each wave is 9.8 mm, and the phase difference between them is 85°.
Key Idea : These waves interfere to produce a sinusoidal traveling wave.
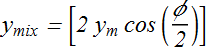
What is the amplitude of the resultant wave due to the interference, and what is the type of this interference?
![]()
What phase difference, in radians and wavelengths, will give the resultant wave an amplitude of 5.9 mm?
Standing Waves
Let us consider interference of two identical waves (green and orange) traveling in opposite direction. Assume that both are in phase means φ = 0 rad.
![]() is traveling along positive x direction and
is traveling along positive x direction and ![]() , is traveling along negative x direction.
, is traveling along negative x direction.
![]()
![]()
Net displacement ![]() of string (blue) due to these waves is given as
of string (blue) due to these waves is given as
![]()
As per trigonometric relation

![]()
You can see this function does not represent a traveling wave as it is not a function of (k x-ω t). This wave is called a standing wave (blue wave).
If two sinusoidal waves of the same amplitude and wavelength travel in opposite directions along a stretched string, their interference with each other produces a standing wave.
Terms Used in a Standing waves
The quantity ![]() can be viewed as the amplitude of oscillation of the string element that is located at position x.
can be viewed as the amplitude of oscillation of the string element that is located at position x.
However, since an amplitude is always positive but sin(kx) can be negative, therefore we take the absolute value of the quantity ![]() to be the amplitude at x.
to be the amplitude at x.
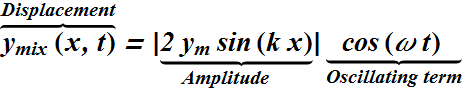
In a traveling sinusoidal wave, the amplitude of the wave is same for all string elements.
For a standing wave, the amplitude of each string element varies with position.
Checkpoint-6: (Interference)
Two waves with the same amplitude and wavelength interfere in three different situations to produce resultant waves with the following equations:
(1) ![]()
(2) ![]()
(3) ![]()
In which situation are the two combining waves traveling (a) toward positive x, (b) toward negative x, and (c) in opposite directions?
Nodes and anti-nodes in Standing waves
In standing wave there are places along the string (green beads), called nodes, where the string never moves.
Halfway between adjacent nodes are anti-nodes (blue beads), where the wave amplitude ![]() of the resultant wave is a maximum.
of the resultant wave is a maximum.
Position of nodes and anti-nodes
Nodes position :
At nodes the wave amplitude ![]() , that is possible when sin(kx) = 0. Therefore corresponding values of kx are given as
, that is possible when sin(kx) = 0. Therefore corresponding values of kx are given as
![]()
By substituting the value of k = 2π/λ, we get the positions of nodes at
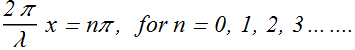
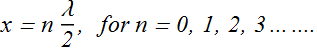
Anti-nodes position :
At anti-nodes the wave amplitude ![]() , that is possible when {sin(kx)}=1. Therefore corresponding values of kx are given as
, that is possible when {sin(kx)}=1. Therefore corresponding values of kx are given as
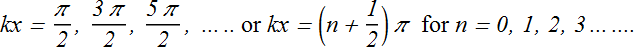
By substituting the value of k = 2π/λ, we get the positions of anti-nodes as
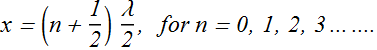
Standing Waves and Resonance
Consider a string stretched between two clamps (such as a guitar string).
Now suppose we send continuous sinusoidal waves of certain frequencies on this string.
We will see that for certain frequencies the interference produce a standing wave pattern with nodes and large anti nodes.
This observation raises few questions.
Questions and Answers:
Standing wave requires two waves traveling in opposite direction. Where from the second wave traveling in opposite direction comes?
Whenever a wave experiences a boundary at the end of the string, it experience reflection. This reflected wave start moving in the opposite direction.
What will be the amplitude of wave at the clamped locations?
Since the string is clamped, so it cannot move and the amplitude of any wave traveling on this string will always be zero at the clamped ends.
We can also say that the clamped parts of the string will always remain nodes for any standing wave on that string.
Can all frequencies produce standing wave on the clamped string?
No.
Which frequencies (or wavelength) can produce standing wave on a clamped string of length L?
We know that position of nodes on a standing wave is given by
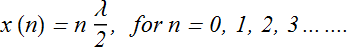
On the clamped string of length L, if the only nodes are those at the clamped ends, then the wavelength λ which can produce standing wave will be related to L as
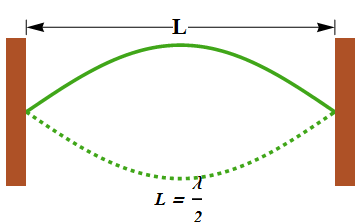
What will be the distance d between first x(0) and second x(1) nodes? It will be
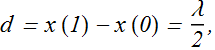
Wavelength λ = 2L can produce standing wave.
If three nodes are present, then the distance between the third and first node should be equal to the length L of the string.
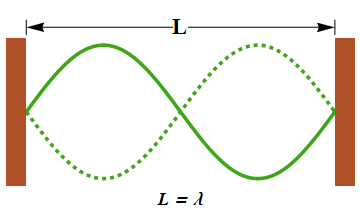
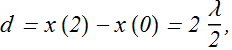
Wavelength λ = 2L/2 = L can produce standing wave.
If four nodes are present, then the distance between the fourth and first node should be equal to the length L of the string.
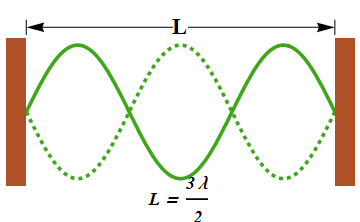
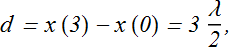
Wavelength λ = 2L/3 can produce standing wave.
That means all the wavelengths given by following equation can form standing wave on a string of length L.
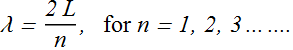
Frequency of standing waves on a clamped string:
If we know the wavelengths which can produce standing wave on a clamped string of length L, we can calculate the corresponding frequencies.
![]()
The frequencies are called resonant frequencies.
Resonant frequencies are integer multiples of the lowest resonant frequency f = v/2L, and are called modes or harmonics of the clamped string.
The oscillation mode with the lowest frequency is called the fundamental mode or the first harmonic.
The collection of all possible oscillation modes is called the harmonic series, and n is called the harmonic number of the nth harmonic.
If the frequency is in the audible range, you can hear the shape of the string.
Resonance can also occur in two dimensions (such as on the surface of the kettledrum) and in three dimensions (such as in the wind-induced swaying and twisting of a tall building).
Checkpoint-7: (Resonance frequencies)
In the following series of resonant frequencies, one frequency (lower than 400 Hz) is missing: 150, 225, 300, 375 Hz.
(a)What is the missing frequency?
(b)What is the frequency of the seventh harmonic?
Key Idea: Difference between two adjacent frequencies is equal to the fundamental frequency
If we assume 150 Hz and 225 adjacent then ![]()
If 225 Hz and 300 Hz are also adjacent then ![]()
If 300 Hz and 375 Hz are also adjacent then ![]()
These observations clearly indicate that 75 Hz is the fundamental harmonic and should be part of the list. Other harmonics will be greater than 400 Hz.
Wave speed on a Stretched String
Instead of the sinusoidal wave let us generate a single symmetrical traveling pulse (Click Play).
The pulse is moving from left to right. Now select "Show disk" and watch.
We observe as if the pulse is generated by moving an imaginary disk under the stretched string, with speed v.
If we move with the disk, the string will appear moving over the disk from right to left with same speed v.
We can use this "moving string over an imaginary disk" model to compute wave speed v.
Observe the wave pulse while moving with speed v, along the imaginary disk.
The peak of string appears to move from right to left (opposite to disk) along a curved path of radius R (disk radius) with tangential (blue arrow) speed v.
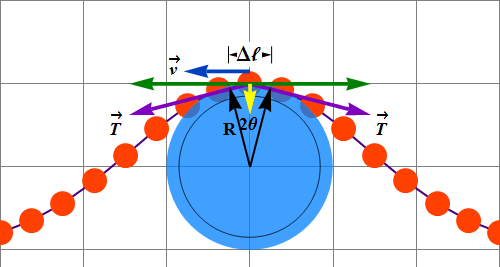
Tension force ![]() (purple arrows) pulls on both sides of the bead (string element of length Δℓ) on the crust of the pulse.
(purple arrows) pulls on both sides of the bead (string element of length Δℓ) on the crust of the pulse.
The horizontal components of tension force T (Green arrows) cancel each other, while the vertical components (Yellow arrows) add up and are producing approximately the net downward force ![]() acting on the bead (string element of length Δℓ).
acting on the bead (string element of length Δℓ).
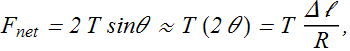
Other force acting on the bead is due to gravity and it is negligible in comparison to tension force.
At the moment, the bead on top is moving in an arc of a circle, therefore the bead is experiencing downward centripetal acceleration a.
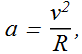
If m is the mass of each bead.
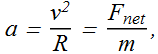
By substituting the value of net downward force we get
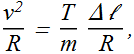
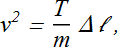
Mass of each bead (string element of length Δ l ) can also be written in terms of linear mass density μ of the string.
![]()
By plugging this value in expression for speed v, we get.
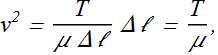
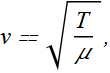
The speed of a wave along a stretched ideal string depends only on the tension and linear density of the string and not on the frequency of the wave.
Checkpoint-8: (Wave on a stretched string)
You send a traveling wave along a particular string by oscillating one end.
(a) If you increase the frequency of the oscillations, do(i) the speed of the wave and the (ii) wavelength of the wave increase, decrease, or remain the same?
(b) If, instead, you increase the tension in the string, do the (i)speed of the wave and the (ii) wavelength of the wave increase, decrease, or remain the same?
Problem-3: (Resonance frequencies)
A 125 cm length of string has mass of 2.00 g and tension 7.00 N.
What is the wave speed for this string?
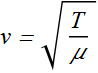
What is the lowest resonant frequency of this string?
![]()
What is the wavelength and frequency of the 5th harmonics?
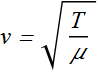
Energy of a wave Along a String
Kinetic Energy
Watch the motion of green and purple string beads (elements) oscillating transversely as a wave pass through it.
The transverse velocity v of these beads is maximum when it is passing through its equilibrium position y = 0 (purple bead position after the simulation stops).
Thus the kinetic energy is maximum at y = 0.
Kinetic energy is zero at ![]() position (green bead position after the simulation stops).
position (green bead position after the simulation stops).
Elastic Potential Energy
Watch the length of springs or thread elements connecting the oscillating beads as a wave pass through it.
When the string element is passing through transverse position y = 0 (purple bead position after the simulation stops), it is getting maximum stretched.
Thus the potential energy will also be maximum at y = 0 (like a spring, more you stretch it more is the potential energy stored).
There is no stretching of the element at ![]() position (green bead position after the simulation stops).
position (green bead position after the simulation stops).
Thus potential energy is also zero at ![]() (maximum amplitude position).
(maximum amplitude position).
In an oscillating string both kinetic energy and potential energy are maximum at y = 0
How to compute Kinetic Energy of a String Element
Consider a wave started passing through a string made up of beads and springs.
Let us assume that space between two adjacent beads is Δx and mass of each bead is m
The kinetic energy ΔK associated with each bead is given as
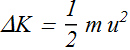
u is the transverse speed of the bead at time t.
![]()
If μ is the linear density of the whole string then mass of each bead can also be written in terms of linear density m = μ Δx, and kinetic energy will be given as
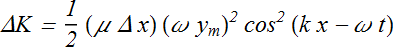
The Rate of Energy (flow)Transmission
If Δ t is the time taken by the wave to reach from green bead to purple bead, then Δt = Δx/v. Where v is the wave speed.
We can say energy has reached from green bead to purple bead in time Δt, thus the rate of kinetic energy flow across the string can be given as
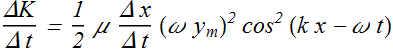
If we replace Δx/Δt by v the rate of kinetic energy flow across the string is
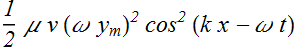
The average power flow of kinetic energy in one cycle (one time period T) can be computed as
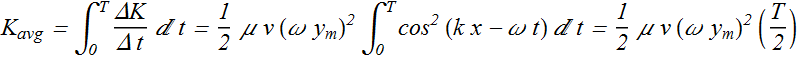
Equal amount of potential energy also flow with kinetic energy, therefore total average energy flowing across the string in one cycle is
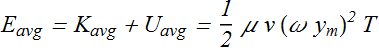
Now the average power flowing across the string will be given as
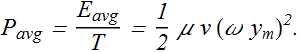
Problem-4: (Energy Transmission)
A string has linear density μ=500g/m and tension T=50.0N. We send a sinusoidal wave with frequency f = 120 Hz and amplitude ![]() along the string.
along the string.
At what average rate does the wave transport energy?
Key Idea : Average rate of energy transport is the average power