Vectors
Objectives
Physics deals with parameters that can be completely described by a number and are known as “scalars”. Temperature and mass are such parameters.
There are many other parameters that require both size (magnitude) and direction and are known as “vectors” . Examples of vectors are displacement, velocity and acceleration.
In this chapter we will learn:
What is a vector
How to draw a vector.
How to write a vector.
When two vectors are equal.
When two vectors are different.
Geometric vector addition and subtraction
Resolving a vector into its components
The notion of a unit vector
Add and subtract vectors by components
Multiplication of a vector by a scalar
The scalar (dot) product of two vectors
The vector (cross) product of two vectors
What is a Vector?
A vector is a quantity that has magnitude and direction.
Simplest example of a vector is the displacement vector which describes the change in position of an object as it moves from one point (start) to other (finish).
Click play and watch displacement of red disk from origin to final position.
How the vector is drawn? (Select show vector)
It is drawn by an arrow (blue arrow) that points from start point to finish point.
The length of the arrow (1.13 m) is proportional to the displacement magnitude.
The direction (45° north of east) of the arrow indicated the displacement direction.
Velocity, acceleration etc. are other examples of vector.
How to write a vector?
In books vectors are written in two ways :
Method 1 : ![]() (using an arrow above)
(using an arrow above)
Method 2 : a (using bold face print )
The magnitude of the vector is indicated by italic print : a
When two vectors are same or equal?
Shift any of the two vectors ![]() and
and ![]() (Click hold and drag).
(Click hold and drag).
A vector can be shifted without changing its length (magnitude) and direction.
The vectors ![]() and
and ![]() are just two shifted vectors with same magnitude and direction, therefore both represent the same vector or we can say
are just two shifted vectors with same magnitude and direction, therefore both represent the same vector or we can say
![]()
Any two vectors with same magnitude and direction, are considered as same vector or equal.
When two vectors are different?
Two vectors with same magnitude but different direction shown in figure (a) are considered different vectors.
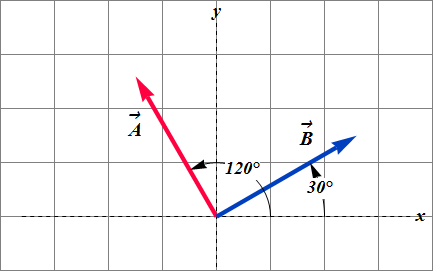 |
| (a) |
 |
| (b) |
Two vectors in same direction but of different magnitude shown in figure (b) are also considered as different vectors.
Checkpoint 1
Which of the following statements, if any, involves a vector?
(a) I walked 2 miles along the beach.
(b) I walked 2 miles due north along the beach.
(c) I jumped off a cliff and hit the water traveling at 17 miles per hour.
(d) I jumped off a cliff and hit the water traveling straight down at 17 miles per hour.
(e) My bank account shows a negative balance of −25 dollars.
Adding Vectors Geometrically
Sum of two vectors is a vector.
![]()
Sketch vector ![]() using an appropriate scale.
using an appropriate scale.
Sketch vector ![]() using the same scale.
using the same scale.
Place the tail of ![]() at the tip of
at the tip of ![]() .
.
The vector ![]() starts from the tail of
starts from the tail of ![]() and terminates at the tip of
and terminates at the tip of ![]() .
.
(Click hold and drag the vectors)
Vector addition is commutative.
![]()
(Click hold and drag the vectors)
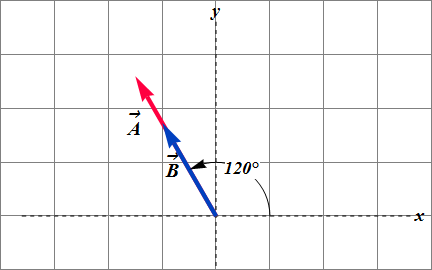
Negative ![]() of a given vector
of a given vector ![]() has the same magnitude as
has the same magnitude as ![]() but opposite direction.
but opposite direction.
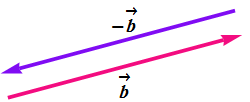
Checkpoint 2
In the following figures, is ![]() ?
?
Components of Vectors
A component of a vector is the projection of the vector on an axis.
The components form the legs of a right triangle whose hypotenuse is the magnitude of the vector.
The process of finding the components of a vector is called resolving the vector.
How to compute component of a vector?
To find the projection of a vector along an axis, we draw perpendicular lines from the two ends of the vector to the axis, as shown.
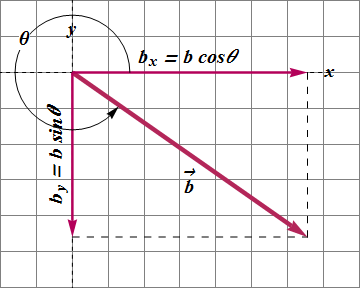
The projection of a vector ![]() on an x axis is its x component
on an x axis is its x component ![]() ).
).
The projection of a vector ![]() on the y axis is the y component
on the y axis is the y component ![]() ).
).
We can find the components of ![]() geometrically from the right triangle.
geometrically from the right triangle.
If θ is the angle that the vector makes with the positive direction of the x axis, and b is the magnitude of ![]() .
.
![]()
How to compute vector magnitude and direction angle?
The magnitude of the vector ![]() in terms of its components
in terms of its components ![]() and
and ![]() is given as
is given as
![]()
For angle θ we can use inverse trigonometric function
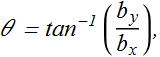
If θ is positive there can be two values
θ = θ if ![]() and
and ![]() both are positive
both are positive
![]() if
if ![]() and
and ![]() both are negative.
both are negative.
If θ is negative there can be two values
![]() if
if ![]() is negative and
is negative and ![]() is positive.
is positive.
![]() if
if ![]() is positive and
is positive and ![]() is negative.
is negative.
Unit Vector
A unit vector is a vector that has a magnitude of exactly 1 and points in a particular direction.
It does not have any dimension or units.
Its sole purpose is to point — that is, to specify a direction.
The unit vectors in the positive directions of the x, y, and z axes are labeled ![]() ,
, ![]() and
and ![]() where the hat ^ is used instead of an overhead arrow as for other vectors
where the hat ^ is used instead of an overhead arrow as for other vectors
How to write vector in unit vector notation?
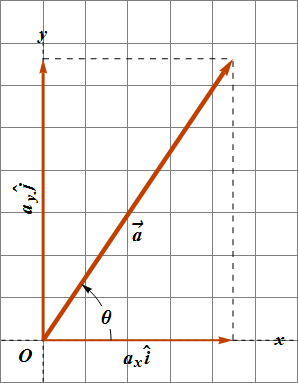
Any vector can be expressed in terms of unit vectors and its components.
A vectors ![]() can be expressed as
can be expressed as
![]()
![]() and
and ![]() are vectors, called the vector components of
are vectors, called the vector components of ![]() .
.
The quantities ![]() and
and ![]() are scalars, called the scalar components.
are scalars, called the scalar components.
A vector component along any axis can be written as the product of the magnitude of the component and unit vector along that axis.
Example-1
A car moves with velocity of magnitude 30.00 m/s in 30° north of east, find its components, write it in terms of unit vectors and verify your results.
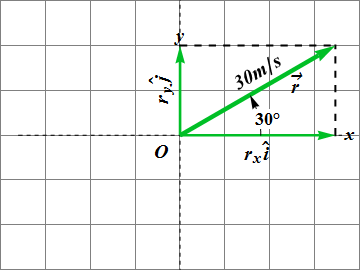
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Verification of results
![]()
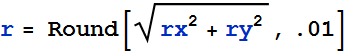
![]()
We know angle of a vector is given as
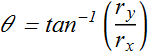
![]()
![]()
Since both x (or i) and y (or j) components are +ve, therefore vector is in 1st quadrant. Hence 30° value is correct.
Example-2
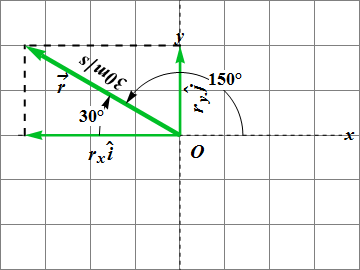
A car moves with velocity of magnitude 30.00 m/s in 30° north of west, find its components, write it in terms of unit vectors and verify your results.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Verification of results
![]()
![]()
![]()
We know angle of a vector is given as
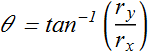
![]()
![]()
Since x (or i) component is –ve and y (or j) component is +ve, therefore vector is in 2nd quadrant. Hence correct value is 180° -30°= 150°.
Example-3
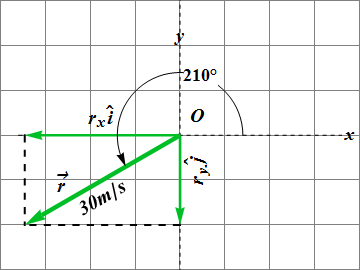
A car moves with velocity of magnitude 30.00 m/s in 30° south of west, find its components, write it in terms of unit vectors and verify your results.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Verification of results
![]()
![]()
We know angle of a vector is given as
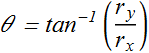
![]()
![]()
Since x (or i) component is –ve and y (or j) component is -ve, therefore vector is in 3rd quadrant. Hence correct value is 180° +30° = 210°.
Example-4
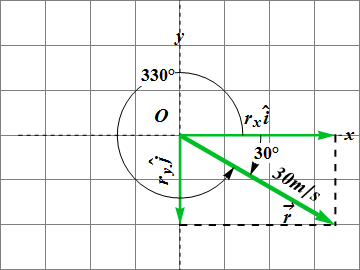
A car moves with velocity of magnitude 30.00 m/s in 30° south of east, find its components, write it in terms of unit vectors and verify your results.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Verification of results
![]()
![]()
We know angle of a vector is given as
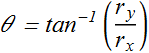
![]()
![]()
Since x (or i) component is +ve and y (or j) component is -ve, therefore vector is in 4th quadrant. Hence correct value is 360° - 30° = 330°.
Component method of vector addition.
Suppose vector ![]() is the sum of two vectors
is the sum of two vectors ![]() and
and ![]() .
.
![]()
First determine the x and y components of ![]() and
and ![]() , relative to a conveniently chosen x, y coordinate system. Be sure to take into account the direction of the components.
, relative to a conveniently chosen x, y coordinate system. Be sure to take into account the direction of the components.
Algebraic sum of x components ![]() and
and ![]() ) of vector
) of vector ![]() and
and ![]() is the x component
is the x component ![]() of sum vector
of sum vector ![]() .
.
![]()
Similarly, the algebraic sum of y components ![]() and
and ![]() ) of vector
) of vector ![]() and
and ![]() is the y component
is the y component ![]() of sum vector
of sum vector ![]() .
.
![]()
Once we know x, y components of ![]() , we can use Pythagorean theorem to determine the magnitude |S| of
, we can use Pythagorean theorem to determine the magnitude |S| of ![]() .
.
![]()
Use inverse tangent function to find the angle that specifies the direction of the resultant vector ![]() .
.
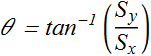
Example-5
Find the vector sum of the three vectors shown in adjacent figure.
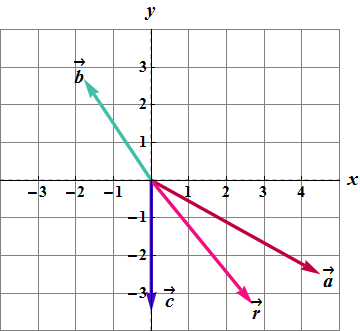
![]()
![]()
![]()
x - component of is obtained by adding x components of all the three vectors.
![]()
![]()
![]()
y - component of is obtained by adding y components of all the three vectors.
![]()
![]()
![]()
Vector ![]() is written as.
is written as.
![]()
Magnitude is computed as
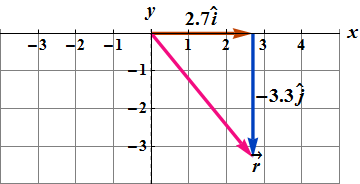
![]()
![]()
![]()
Angle is computed as
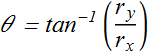
![]()
![]()
Since x (or ![]() ) component is +ve and y (or
) component is +ve and y (or ![]() ) component is -ve, therefore vector is in IVth quadrant. Hence correct value is 360° - 51° = 309.
) component is -ve, therefore vector is in IVth quadrant. Hence correct value is 360° - 51° = 309.
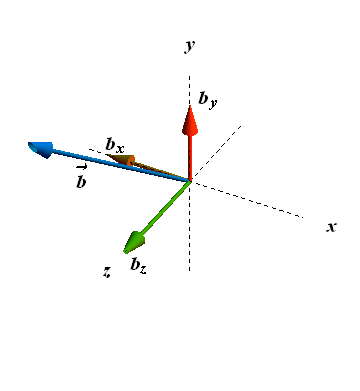
Vector in three dimension
A vector ![]() (blue vector) in three dimension has three components and is written as
(blue vector) in three dimension has three components and is written as
![]()
Vectors and the laws of physics
If ![]() is a vector, what happens if we rotate or translate the coordinate system?
is a vector, what happens if we rotate or translate the coordinate system?
(Click hold and drag for translation)
Note : Here we are rotating the coordinate system, not the vector.
What we learn?
Vectors do not depend on the location of the origin or on the orientation of the axes.
The components of vector change with rotation of axis.
Which component pair represents the vector?
All the component pairs represent same vector because the magnitude and direction of vector does not change.
Components of a vector are dependent on choice of coordinate system but vector is independent of choice of coordinate system.
All relations of physics are independent of the choice of coordinate system.
Multiplying Vectors
Multiplying a Vector by a Scalar
Multiplication of vector ![]() by a scalar s results in a new vector
by a scalar s results in a new vector ![]() .
.
![]()
In the component form multiplication is given as
![]()
OR
![]()
The magnitude of new vector is given by.
![]()
We can also get the magnitude of ![]() from the component method.
from the component method.
![]()
If s>0 vector ![]() has the same direction as vector
has the same direction as vector ![]() .
.
If s<0 vector ![]() has a direction opposite to that of vector
has a direction opposite to that of vector ![]() .
.
Multiplying a vector by a vector
There are two ways to multiply a vector by a vector:
The Scalar Product
The Vector Product
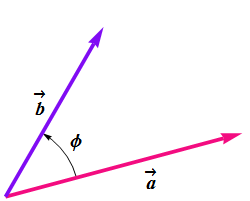
The scalar product
Also known as "Dot" product.
The scalar product ![]() of two vectors
of two vectors ![]() and
and ![]() is a scalar and is given by
is a scalar and is given by
![]()
where φ is the shorter angle between the two vectors.
Commutative law applies to a scalar product
![]()
Dot product in unit vector notation
In unit vector notation dot product is written as
![]()
![]()
This product has nine terms out of which magnitude of six terms will be zero because
![]()
Only three terms will be non-zero because
![]()
Therefore
![]()
The vector product
Also known as “cross” product.
The vector product ![]() of two vectors
of two vectors ![]() and
and ![]() is a vector.
is a vector.
The magnitude of vector ![]() is given by
is given by
![]()
where φ is the shorter angle between the two vectors.
The direction of ![]() is perpendicular to the plane P defined by the vectors
is perpendicular to the plane P defined by the vectors ![]() and
and ![]() .
.
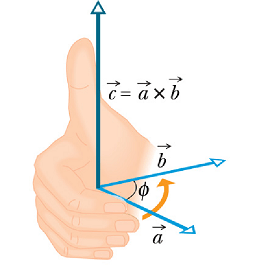
Direction of product vector is given by the right hand rule :
Place the vector and tail to tail
Rotate fingers of the right hand along the shortest angle from ![]() to
to ![]() .
.
The direction of thumb will be the direction of cross product vector (![]() ).
).
Commutative law does not apply to the vector product
![]()
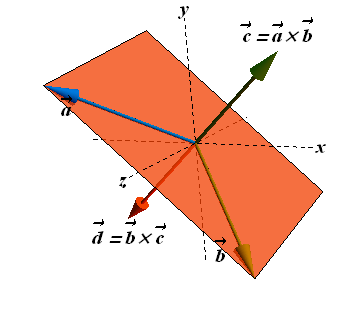
![]()
Cross product vectors ![]() or
or ![]() of are always
perpendicular to the plane containing vectors
of are always
perpendicular to the plane containing vectors ![]() and
and ![]() .
.
Cross product in unit vector notation
In unit vector notation vector product is written as
![]()
![]()
This product has nine terms out of which magnitude of three terms will be zero because
![]()
Similarly cross product of other six terms will be non zero because
![]()
How to compute direction of cross product of unit vector?
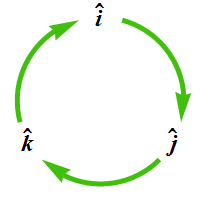
Look at the adjacent figure.
Cross product of two unit vector will be third unit vector.
If you are moving in clock wise direction the sign will be positive.
![]()
If you are moving in anti-clock wise direction, the sign will be negative.
![]()
Therefore cross product ![]() is given as
is given as
![]()
![]()
![]()
Cross product computation Method
![]() can also be calculated by taking det of following matrix.
can also be calculated by taking det of following matrix.
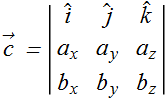
components are computed as below.
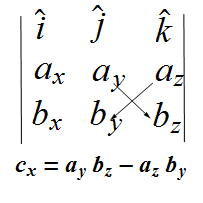 |
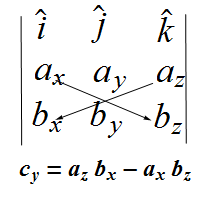 |
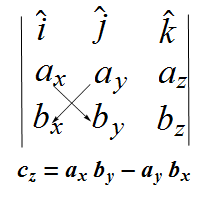 |
As per this rule, the components of vector ![]() are given as
are given as
![]()
