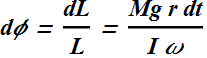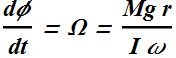Torque and Angular Momentum
In this chapter we will learn about torque and angular momentum.
After finishing this chapter we should know following topics:
Torque for rotation (symbol τ)
Newton’ s second law for rotational motion.
Work and rotational kinetic energy.
General definition of torque for a particle that moves along any path relative to a fixed point.
Angular Momentum of single particles and systems or particles.
Relation between angular momentum and torque (Newton’s Second Law in angular Form).
Rotational and translational angular momentum.
Relation between Angular Momentum and Angular velocity
Conservation of angular Momentum.
Applications of the conservation of angular momentum.
How a Gyroscope works?
What is Torque?
Torque measures the ability of a force to rotate an object.
Let us try to open (rotate) the door by applying a force ![]() .
.
Will the force in its present direction be able to open (rotate) the door?
Click "Open door" button and see the answer.
Now rotate the force by 90 °, will it be able to open (rotate) the door?
Click "Open door" button and see the answer.
Switch to the top view and see the direction of force vector with respect to rotating path (blue dots).
We observed that when a force acts tangentially to the rotating path of an object, it can rotate the object.
Now change the position of the force.
When the force is acting closer to the rotating axis, will it be easy or more difficult to rotate (open) the door?
From this simulation we can conclude.
Applied force ![]() is able to rotate the door only when it acts tangentially to the path of rotation.
is able to rotate the door only when it acts tangentially to the path of rotation.
Ability of the force to rotate the object depends on the position of the force from the rotating axis.
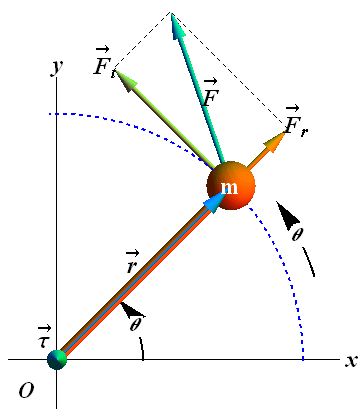
Torque
Consider a simple rigid body, with a particle of mass m attached to a mass less rod, free to rotate about an axis through O.
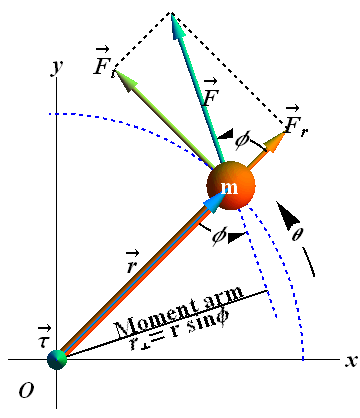
A force ![]() is applied to the particle at a position
is applied to the particle at a position ![]() .
.
Angle between ![]() and
and ![]() is φ.
is φ.
Only tangential component ![]() is capable of rotating the object.
is capable of rotating the object.
Ability to rotate also depends on the position ![]() of action.
of action.
This ability to rotate is called torque and its symbol is τ.
![]()
Another equivalent way of writing torque is
![]()
where ![]() is the perpendicular distance between the rotation axis at O and an extended line running through
is the perpendicular distance between the rotation axis at O and an extended line running through ![]() . This extended line is called the line of action of
. This extended line is called the line of action of ![]() , and
, and ![]() is called the moment arm of
is called the moment arm of ![]() .
.
Torque ![]() is vector quantity and can be written as
is vector quantity and can be written as
![]()
SI units of Torque:
The SI unit of torque is the Newton-meter (N·m).
Caution: The Newton-meter is also the unit of work.
Torque and work, however, are quite different quantities and must not be confused.
Work is often expressed in joules (1 J = 1 N m), but torque is never expressed in joules.
Problem 1: (Work and rotational kinetic energy)
A rod is pivoted about its center. A 5 N force is applied 4m from the pivot and another 5 N force is applied 2m from the pivot, as shown.
What is the magnitude of the total torque about the pivot (in N·m)?
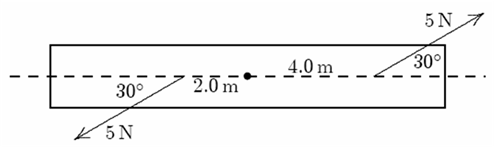
Solution :
![]()
![]()
Newton’s Second law for Rotation
Torque can cause rotation of a rigid body as force can accelerate a body.
Net torque ![]() acting on a rigid body produces angular acceleration α and these two quantities can be related by Newton's second law for rotation.
acting on a rigid body produces angular acceleration α and these two quantities can be related by Newton's second law for rotation.
![]()
Let us prove the above relation. Consider the system shown in figure.
Tangential force ![]() is related to tangential acceleration
is related to tangential acceleration ![]() as
as ![]() . Therefore torque τ can be written as
. Therefore torque τ can be written as
![]()
Tangential acceleration ![]() is related to angular acceleration α as
is related to angular acceleration α as
![]()
Therefore
![]()
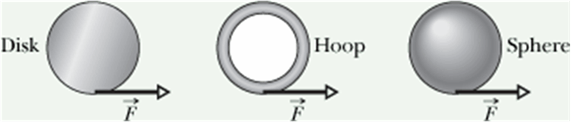
Checkpoint-1: (Newton’s Law for rotation)
A uniform disk, a thin hoop, and a uniform sphere, all with the same mass and same outer radius, are each free to rotate about a fixed axis through its center. Assume the hoop is connected to the rotation axis by light spokes. With the objects starting from rest, identical forces are simultaneously applied to the rims, as shown.
Rank the objects according to their angular accelerations, least to greatest.
Key Idea:
![]()
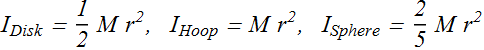
Work and Rotational Kinetic Energy
Suppose a torque τ change the angular velocity of a rotating object from its initial value ![]() to
to ![]() .
.
Therefore we can say that the torque has changed the rotational kinetic energy of the rotating object.
The change in rotational kinetic energy ΔK can be given as
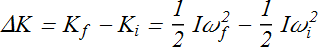
Change in kinetic energy is equal to the work W done by the torque.
![]()
The work dW done due to tangential component of force ![]() , in moving the particle by a distance ds along the circular path is
, in moving the particle by a distance ds along the circular path is
![]()
By substituting the value of ds in terms of angular displacement dθ, we get
![]()
Therefore work done by torque in moving the object from its initial angular position ![]() to final angular position
to final angular position ![]() .
.
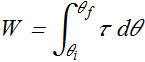
Similarly, the rate at which the work (Power) is done by torque is given as is power
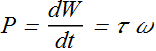
Problem 2: (Work and rotational kinetic energy)
A disk has a rotational inertia of ![]() and a constant angular acceleration of
and a constant angular acceleration of ![]() .
.
If it starts from rest, what will be the work done during the first 5.0 s by the net torque acting on it?
Solution :
Initial angular velocity ![]() , therefore initial kinetic energy is zero.
, therefore initial kinetic energy is zero.
We need to calculate final angular velocity, final kinetic energy to compute work done.
![]()
![]()
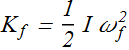
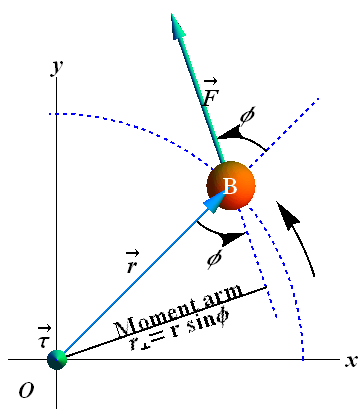
Torque (A general Definition)
For an object B rotating in a plane, we have defined torque ![]() as
as
![]()
Here ![]() is the position from the center of rotation and
is the position from the center of rotation and ![]() is the force acting on that object.
is the force acting on that object.
This definition can be expanded to any individual particle A that moves along any path (circle, ellipse or straight line) due to influence of a force ![]() .
.
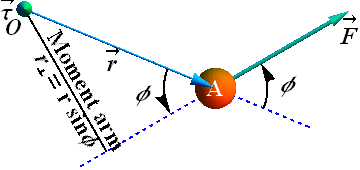
The torque on A about any point O is again defined as
![]()
Magnitude of the torque ![]() of the particle, relative to any point O is given as
of the particle, relative to any point O is given as
![]()
![]()
![]()
We have three formulas to compute magnitude of torque.
φ is the smaller angle between ![]() and
and ![]() .
.
![]() is the perpendicular distance from point O to the line of action (dashed blue line). It is called moment arm.
is the perpendicular distance from point O to the line of action (dashed blue line). It is called moment arm.
![]() is the tangential component of the force with respect to
is the tangential component of the force with respect to ![]() .
.
Torque has meaning only with respect to a specified location. If a different location (O) is chosen, ![]() will change, the value of the torque is usually changed too.
will change, the value of the torque is usually changed too.
Angular Momentum
When a particle is moving with a linear momentum ![]() , the angular momentum
, the angular momentum ![]() of the particle, relative to a location A is defined as
of the particle, relative to a location A is defined as
![]()
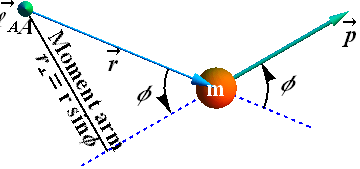
Here ![]() is the position vector of the particle measured from location A.
is the position vector of the particle measured from location A.
Magnitude of the angular momentum ![]() of the particle, relative to a location A is given as
of the particle, relative to a location A is given as
![]()
![]()
![]()
We have three formulas to compute magnitude of angular momentum.
φ is the smaller angle between ![]() and
and ![]() .
.
![]() is the perpendicular distance from location A to the line of motion (dashed blue line). It is called moment arm.
is the perpendicular distance from location A to the line of motion (dashed blue line). It is called moment arm.
![]() is the tangential component of the momentum with respect to
is the tangential component of the momentum with respect to ![]() .
.
Angular momentum has meaning only with respect to a specified location. If a different location (A) is chosen, ![]() will change, the value of the angular momentum is usually changed too.
will change, the value of the angular momentum is usually changed too.
SI units for angular momentum
SI units for angular momentum are written as
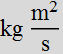
Since angular momentum ![]() of the particle, relative to a location A is given as
of the particle, relative to a location A is given as
![]()
Units for position r is meter (m) and units for linear momentum (p=m v) are kilogram meter/second (kg m/s).
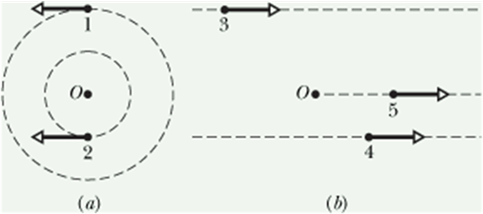
Checkpoint-2: ( Angular Momentum)
In part a of the figure, particles 1 and 2 move around point O in opposite directions, in circles with radii 2 m and 4 m. In part b, particles 3 and 4 travel in the same direction, along straight lines at perpendicular distances of 4 m and 2 m from point O. Particle 5 moves directly away from O. All five particles have the same mass and the same constant speed.
(a) Rank the particles according to the magnitudes of their angular momentum relative to point O, greatest first.
(b) Which particles have negative angular momentum relative to point O?
Hint : ![]()
Newton’s Second Law in Angular Form
As per Newton's second law, time derivative of linear momentum is equal to net external force:
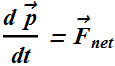
Let us see what the time derivative of angular momentum ![]() relative to point A, turn out to be?
relative to point A, turn out to be?
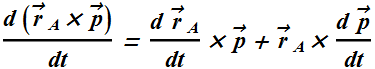
Now ![]() , therefore the first term on right hand side in above equation can be written as
, therefore the first term on right hand side in above equation can be written as
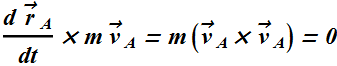
Therefore the time rate of change of angular momentum is given as
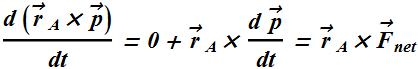
![]() is defined as the net torque acting on the object relative to location A.
is defined as the net torque acting on the object relative to location A.
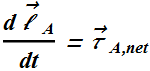
Time derivative of angular momentum of an object, relative to point A, is equal to net external torque relative to same point A:
Another way of writing SI units of Angular Momentum :
As per above relation, SI units for angular momentum can also be written as
Newton-meter (N·m) × s.
![]()
Since
![]()
Angular Momentum of multi-particle systems
Total angular momentum ![]() of a system of particles relative to a point A, is the vector sum of the angular momentum
of a system of particles relative to a point A, is the vector sum of the angular momentum ![]() of the individual particles relative to same point A.
of the individual particles relative to same point A.
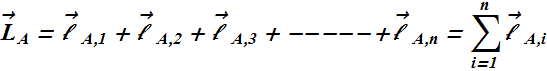
The change in total angular momentum with time will be equal to the net sum of external torques (relative to point A) acting on individual particles.
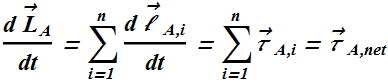
Rotational Angular Momentum*
Consider a multi-particle system of three particles with linear momentum ![]() ,
, ![]() and
and ![]() .
.
Angular momentum of each particle, relative to a location A is defined as
![]()
Here ![]() ,
, ![]() and
and ![]() are positions of particles 1, 2 and 3 with respect to point A.
are positions of particles 1, 2 and 3 with respect to point A.
Total angular momentum ![]() of the system relative to point A will be vector sum of angular momentum of the individual three particles relative to same point A.
of the system relative to point A will be vector sum of angular momentum of the individual three particles relative to same point A.
![]()
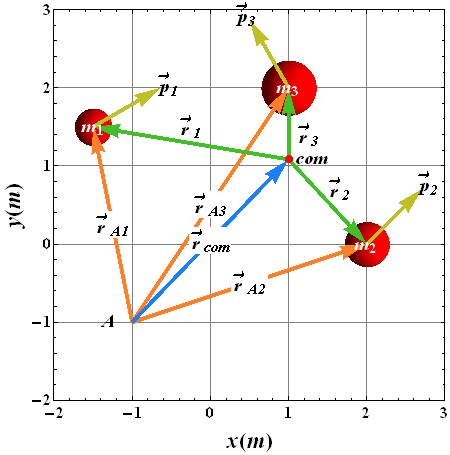
If ![]() is the position of center of mass of the system with respect to point A, the position vectors
is the position of center of mass of the system with respect to point A, the position vectors ![]() ,
, ![]() and
and ![]() can be written in terms of
can be written in terms of ![]() .
.
![]()
Here ![]() ,
, ![]() and
and ![]() are positions of particles with respect to center of mass (com) of the system.
are positions of particles with respect to center of mass (com) of the system.
By substituting the values of ![]() ,
, ![]() and
and ![]() , the expression of total angular momentum
, the expression of total angular momentum ![]() of the system can be rewritten as
of the system can be rewritten as
![]()
Here first part in above equation is called rotational angular momentum ![]() of the system relative to its center of mass. Second part is called translational angular momentum
of the system relative to its center of mass. Second part is called translational angular momentum ![]() of the center of mass of the system relative to point A.
of the center of mass of the system relative to point A.
![]()
![]()
Here ![]()
![]() , is the total linear momentum of the system or linear momentum of the center of mass.
, is the total linear momentum of the system or linear momentum of the center of mass.
Therefore total angular momentum ![]() of a system relative to any point A, is equal to the vector sum of rotational angular momentum
of a system relative to any point A, is equal to the vector sum of rotational angular momentum ![]() of the system, and the translational angular momentum
of the system, and the translational angular momentum ![]() of the center of mass of the system relative to the point A.
of the center of mass of the system relative to the point A.
![]()
For a stationary system with total linear momentum ![]() , the total angular momentum
, the total angular momentum ![]() relative to any point A in space will be equal to its rotational angular momentum
relative to any point A in space will be equal to its rotational angular momentum ![]() .
.
When linear momentum of a system ![]() , the total angular momentum
, the total angular momentum ![]() relative to any point A in space is always equal to its rotational angular momentum
relative to any point A in space is always equal to its rotational angular momentum ![]() .
.
![]()
Will an object with finite angular Momentum always rotate?
A system with finite rotational angular momentum ![]() will always rotate or spin about an axis passing through its center of mass.
will always rotate or spin about an axis passing through its center of mass.
Examples of Rotational angular momentum:
Spinning of Earth bout its axis.
Spinning of electrons about their axis.
A system with finite translational angular momentum ![]() about a point A, may or may not rotate or revolve
around point A.
about a point A, may or may not rotate or revolve
around point A.
In the following simulation there are two disks with same translational angular momentum ![]() relative to point A. Release (click play) and watch, one revolves around A, while other goes along a straight line.
relative to point A. Release (click play) and watch, one revolves around A, while other goes along a straight line.
Examples of Translational angular momentum:
Revolving of Earth around sun (an axis passing through a point in sun).
Orbiting of electrons around the nucleus in an atom.
Linear motion of a rocket with respect to a point on Earth or anywhere in space.
Direction of Angular Momentum and Angular velocity.
Angular velocity ![]() of a rotating object is always parallel to its axis of rotation.
of a rotating object is always parallel to its axis of rotation.
Rotational Angular momentum ![]() of a rigid body is not necessarily parallel to its axis of rotation or parallel to its angular velocity
of a rigid body is not necessarily parallel to its axis of rotation or parallel to its angular velocity ![]() .
.
This is because, moment of inertia/rotational inertia of a rigid body changes with the choice of the rotation axis (moment of inertia is a 3×3 tensor).
A rigid body of any shape, possesses three mutually perpendicular axes through the center of mass. These axes are called principal axes of the body, and they have an important property.
When axis of rotational is one of the principal axis, rotational angular momentum ![]() is parallel to axis of rotation or parallel to the angular velocity
is parallel to axis of rotation or parallel to the angular velocity ![]() .
.
![]()
![]() is the moment of inertia about the principal axis.
is the moment of inertia about the principal axis.
For a body having axes of symmetry, the principal axes are along the symmetry axes.
What if ![]() is not parallel to one of the principal axes?
is not parallel to one of the principal axes?
We can choose a coordinate system with x, y and z-axes along the principal axes of a rigid body with corresponding moment of inertia ![]() ,
, ![]() and
and ![]() the components of the rotational angular momentum
the components of the rotational angular momentum ![]() about these axes can be related to corresponding components of angular velocity
about these axes can be related to corresponding components of angular velocity ![]() as below.
as below.
![]()
Above relations are only valid when x, y, z-axes are the principal axes of the rigid body.
![]()
Above relation clearly indicates that directions of ![]() and
and ![]() are not necessarily parallel to each other as moment of inertia
are not necessarily parallel to each other as moment of inertia ![]() ,
, ![]() and
and ![]() along each principal axes, can have different values.
along each principal axes, can have different values.
Rotational kinetic energy ![]() of a rotating rigid object can be related to its rotational angular momentum
of a rotating rigid object can be related to its rotational angular momentum ![]() and its angular velocity
and its angular velocity ![]() .
.
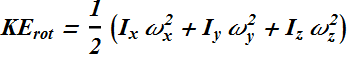
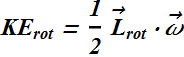
Examples of rotation axis.
If the rotation axis is not the symmetric axis or one of the principal axes, as shown in the simulation, the angular momentum ![]() and angular velocity
and angular velocity ![]() will not be in the same direction.
will not be in the same direction.
You can see that angular momentum vector ![]() continually change direction (wobbling) and requires a non-zero torque (In a rotating object, this is applied to the axle by the bearings).
continually change direction (wobbling) and requires a non-zero torque (In a rotating object, this is applied to the axle by the bearings).
To make ![]() parallel to
parallel to ![]() , we can add another identical object to balance it, now the rotation axis becomes a symmetric axis and is parallel to one of the principal axes, (select balance).
, we can add another identical object to balance it, now the rotation axis becomes a symmetric axis and is parallel to one of the principal axes, (select balance).
You can see that the components of the two angular momentums, perpendicular to rotation axis (red arrows), cancel each other while components of the two angular momentums, parallel to rotation axis (blue arrows), adds up to give total angular momentum.
Net angular momentum now points in the direction of ![]() or points along the rotation axis and does not change direction.
or points along the rotation axis and does not change direction.
Car tires must be carefully balanced to make axis of rotation axis one of the principal axes (symmetric axis). This makes rotation more efficient, prevents wobbling and damage of bearings.
Checkpoint-3: (Angular momentum of a rotating rigid object)
In the figure, a disk, a hoop, and a solid sphere are made to spin about fixed central axes (like a top) by means of strings wrapped around them, with the strings producing the same constant tangential force ![]() on all three objects. The three objects have the same mass and radius, and they are initially stationary.
on all three objects. The three objects have the same mass and radius, and they are initially stationary.
(a) Rank the objects according to their angular momentum about their central axes and
(b) Rank the objects according to their angular speed, greatest first, when the strings have been pulled for a certain time t.
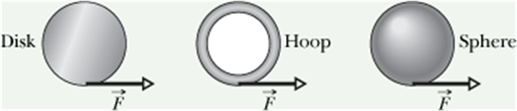
Hint : ![]() and L=I ω
and L=I ω
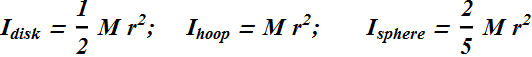
negative x direction
positive x direction
negative y direction
positive z direction
negative z direction
Conservation of Angular Momentum
According to Newton’s second law.
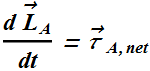
When the applied external net torque ![]() . .
. .
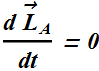
That means angular momentum ![]() is constant.
is constant.
This is called law of conservation of momentum.
If the net external torque ![]() relative to a point A, acting on a system is zero, the angular momentum
relative to a point A, acting on a system is zero, the angular momentum ![]() relative to point A, of the system remains constant, no matter what changes take place within the system.
relative to point A, of the system remains constant, no matter what changes take place within the system.
![]()
If the component of the net external torque ![]() relative to a point A acting on a system along a certain axis is zero, then the component of the angular momentum
relative to a point A acting on a system along a certain axis is zero, then the component of the angular momentum ![]() relative to point A, of the system along that axis cannot change, no matter what changes take place within the system.
relative to point A, of the system along that axis cannot change, no matter what changes take place within the system.
![]()
![]()
![]()
The spinning person:
A rotating person changes from initial position (a) to final position (b).
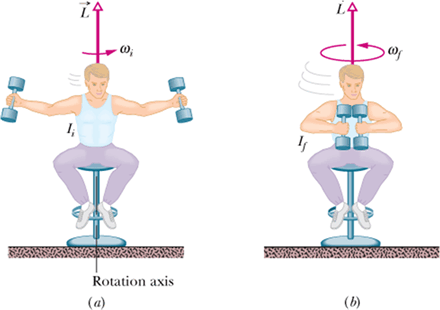
Angular momentum of the system ![]() will remain constant as no net external torque is acting on the system.
will remain constant as no net external torque is acting on the system.
In final position (b) rotational inertia ![]() decreases means
decreases means ![]() .
.
Since magnitude of L = I ω, therefore ![]()
The springboard diver:
The diver’s angular momentum ![]() is constant throughout the dive, being represented by ⊗ the tail of an arrow that is perpendicular to the plane of the figure.
is constant throughout the dive, being represented by ⊗ the tail of an arrow that is perpendicular to the plane of the figure.
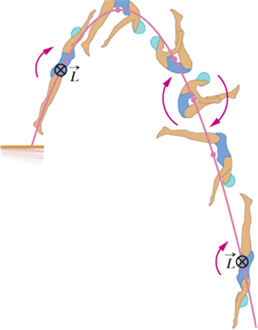
When the diver brings her hands and legs closer, her rotational inertia I reduces.
Since L = I ω, therefore at that time angular velocity ω increases.
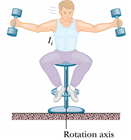 |
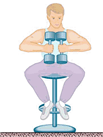 |
By bringing the dumbbells inward, Joe exerts a torque on the stool.
By bringing the dumbbells inward, Joe decreases the moment of inertia.
By bringing the dumbbells inward, Joe increases the angular momentum.
By bringing the dumbbells inward, Joe increases the moment of inertia.
By bringing the dumbbells inward, Joe decreases the angular momentum.
Can you answer?
Look at the video.
Why spinning wheel stays in vertical position?
How a Gyroscope works?
A spinning wheel is called a Gyroscope.
What happens when wheel is not spinning?
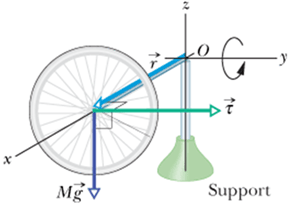
We know according to Newton`s second law ![]()
When the wheel is not spinning it does not have any angular momentum along its axis (x-axis) or along any direction.
Gravitational force acting on its center of mass will produce a torque ![]() , which will try to rotate it along y-axis. In other words torque tries to change its angular momentum from zero to a finite value. The magnitude of
, which will try to rotate it along y-axis. In other words torque tries to change its angular momentum from zero to a finite value. The magnitude of ![]() is
is
![]()
The wheel will fall due to this rotation around y-axis.
What happens when Gyroscope wheel is spinning?
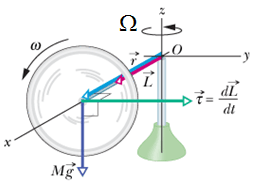 |
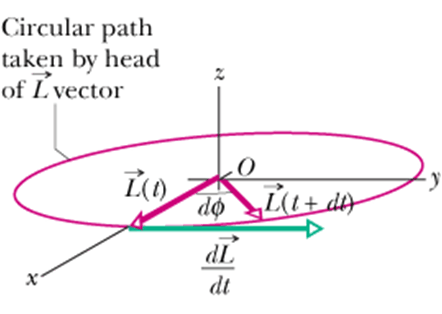 |
When the wheel is rapidly spinning, it has a finite angular momentum ![]() along its rotation axis (x-axis).
along its rotation axis (x-axis).
Torque ![]() due to gravitational force is acting along y-axis.
due to gravitational force is acting along y-axis.
Since torque is acting normal to ![]() , therefore it can only change direction of the angular momentum vector
, therefore it can only change direction of the angular momentum vector ![]() not magnitude.
not magnitude.
This will cause rotation of ![]() or precession of the wheel around z-axis.
or precession of the wheel around z-axis.
We see now gravitational force is the cause of precession of the wheel, instead of its fall.
Now we can calculate the precession rate Ω.
![]()