Rolling
In this chapter we will learn about different aspects of rolling objects.
After finishing this chapter we should know following topics:
Rolling of circular objects.
Relation between linear velocity of a rolling object and its angular velocity.
Rolling as a combination of pure Translation & Rotation.
Kinetic energy of rolling objects.
Importance of friction in rolling objects.
Computation of linear acceleration of few rolling objects.
Can you answer?
A circular wheel and a rectangular block were let to go down (Click start) from the top (height h) of an incline. Both the objects are of same material and have same mass m. If energy loss due to friction is negligible, which one will arrive first to the ground?
What is rolling?
When an object rolls smoothly (without slipping) along a surface. The center of the object (blue point) moves in a straight line with velocity ![]() while a point (red point) on the rim rotates.
while a point (red point) on the rim rotates.
Without slipping means the velocity of point of contact with horizontal surface, should always be zero.
What will be ![]() (center of mass velocity) of a rolling object?
(center of mass velocity) of a rolling object?
Roll (Click roll) the wheel of radius R.
Suppose the wheel covers distance s in time t, the magnitude of velocity ![]() of the center of mass of the wheel is
of the center of mass of the wheel is
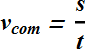
When the roiling wheel rotates by an angle θ the linear distance s covered by the wheel is equal to the distance from point A to B on the wheel rim.
![]()
According to definition of angle θ
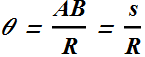
Above equation can be rewritten as
![]()
Since radius of the wheel R is a constant, therefore the magnitude of velocity of the center of mass of the wheel ![]() , can be rewritten as
, can be rewritten as
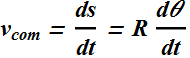
For a rotating wheel, angular velocity ω is given as
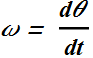
Therefore velocity of the center of mass of a rolling wheel ![]() , is related to its angular velocity ω.
, is related to its angular velocity ω.
![]()
Similarly the linear acceleration of the center of mass of a rolling wheel ![]() is related to its angular acceleration α.
is related to its angular acceleration α.
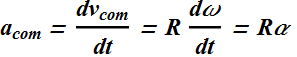
The velocity ![]() and acceleration
and acceleration ![]() of the center of mass of a smoothly rolling wheel, are respectively related to the angular velocity ω and angular acceleration α of the wheel.
of the center of mass of a smoothly rolling wheel, are respectively related to the angular velocity ω and angular acceleration α of the wheel.
What is the velocity of different points of a rolling object?
Look at the photograph of a rolling bicycle wheel.

What we observe?
The spokes near the wheel's top are more blurred than those near the bottom because the top ones are moving faster.
For smooth rolling (without slipping), point touching the ground should have zero velocity.
Rolling: Combination of pure Translation & Rotation
This complicated velocity pattern of a rolling object can be simplified by treating rolling as a combination of pure translation and pure rotation.
Watch a translating wheel without rotation. (Select Translation and click Play)
We observe that velocity of the wheel at point T, O and P is same.
![]()
Watch now a rotating wheel of radius R and angular velocity ω about a stationary axis O. (Select Rotation and click Play)
Velocity of a wheel at point T, O and P is
![]()
Watch a rolling (Translation + Rotation) wheel. (Select combine and click Play)
Now velocity of the wheel at point T, O and P is sum of two velocities due to rotation and translation.
![]()
For a smoothly rolling (without slipping) object ![]() , therefore velocity of the wheel at point T, O and P are
, therefore velocity of the wheel at point T, O and P are
![]()
The angular acceleration of the wheel must be zero ![]() .
.
The tangential velocity is the same for all points on the wheel.
The linear velocity for all points on the rim of the wheel is non-zero.
The tangential velocity is the same for all points on the rim of the wheel.
There is no slipping at the point where the wheel touches the surface on which it is rolling.
Checkpoint-1: (Rolling)
The rear wheel on a clown’s bicycle has twice the radius of the front wheel.
(a) When the bicycle is moving, is the linear speed at the very top of the rear wheel greater than, less than, or the same as that of the very top of the front wheel?
(b) Is the angular speed of the rear wheel greater than, less than, or the same as that of the front wheel
Hints :
Linear speed at the top of a smoothly rolling wheel is equal to twice the translational speed ![]() of the Center of mass of the wheel.
of the Center of mass of the wheel.
Is the ![]() of two wheels of a bicycle same or different?
of two wheels of a bicycle same or different?
Angular speed ω of a rolling wheel is related to the linear speed v of a point on its radius as
![]()
Kinetic Energy of Rolling
Rolling is a combination of translation and rotation.
A rolling object has two types of kinetic energies: a rotational kinetic energy due to its rotation about its center of mass and a translational kinetic energy due to translation of its center of mass.
If a wheel of mass M is rotating with an angular speed ω around an axis passing through its center, the kinetic energy due to rotation ![]() is related to its rotation Inertia
is related to its rotation Inertia ![]() as
as
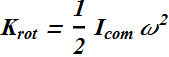
Now the wheel also has a linear velocity ![]() , so its Kinetic energy
, so its Kinetic energy ![]() due to linear motion will be
due to linear motion will be
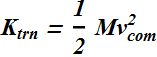
The total Kinetic energy K of such a rolling wheel will be sum of these two kinetic energies.
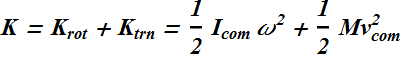
Friction and Rolling
How we start rolling of a bicycle?
First we start rotating (click play to start) the wheels by applying torque on the wheel.
If α is the angular acceleration of the rotating wheel of radius R, the tangential accelerations at points T, and P are given as
![]()
For smooth rolling, the velocity at point P should be zero.
How that is possible?
How to find out direction of friction force for any rolling object?
Checkpoint-2: (Rolling)
A circular wheel and a rectangular block were let to go down (Click start) from the top (height h) of a frictionless incline. Both the objects are of same material and have same mass m. Which one will arrive first to the ground?
Rolling down a Ramp
Consider a wheel of mass M and radius R rolling smoothly down a ramp at an angle θ, along x axis.
What will be the direction of friction?
Without friction, the disk will slide down, therefore direction of force of friction ![]() will be up (select with friction)
will be up (select with friction)
As per Newton's second law, the net force acting on center of mass of the wheel is related to the translational acceleration ![]() of its center of mass.
of its center of mass.
![]()
Do we know the value of force of friction ![]() ?
?
Remember ![]() is static force of friction (It is not maximum static force of friction
is static force of friction (It is not maximum static force of friction ![]() ). When static force of friction
). When static force of friction ![]() , the wheel will start
slipping.
, the wheel will start
slipping.
How to get the value of ![]() ?
?
Since there is rotational motion therefore there should be net torque ![]() acting on the body.
acting on the body.
Three forces are acting on the body, static friction ![]() ,
, ![]() and
and ![]() . Torque due to
. Torque due to ![]() and
and ![]() is zero (these forces are passing through the axis of rotation). Therefore net torque is only due to force of friction
is zero (these forces are passing through the axis of rotation). Therefore net torque is only due to force of friction ![]() .
.
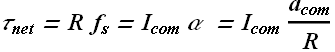
Negative sign is the sign of position vector as R will points down ward from center of mass position.
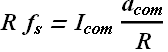
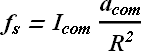
By substituting the value of ![]() in first equation we get
in first equation we get
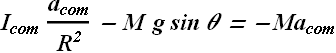
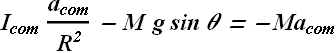
By solving above equation we get value of ![]() .
.
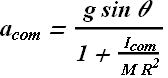
The Yo-Yo
Instead of rolling down a ramp at angle θ with the horizontal, the yo-yo rolls down a string at angle θ= 90° with the horizontal.
Instead of rolling on its outer surface at radius R, the yo-yo rolls on an axle of radius ![]() .
.
Instead of being slowed by frictional force ![]() , the yo-yo is slowed by the tension force T on it from the string.
, the yo-yo is slowed by the tension force T on it from the string.
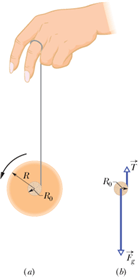
Therefore rolling acceleration ![]() of the Yo-Yo is
of the Yo-Yo is
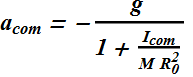
the cylinder will reach the bottom first.
the block will reach the bottom first.
the block will reach the bottom with the greater kinetic energy.
the cylinder will reach the bottom with the greater kinetic energy.
both the block and the cylinder will reach the bottom at the same time.
