Potential Energy

Objectives

In this chapter we will learn the following concepts:

Conservative and non-conservative forces.

Multi-particle energy has three parts:

Rest energy

Kinetic Energy

Potential energy

Potential energy is the interaction energy of pairs of particles with in a multi-particle system.

Learn to compute potential energy.

Relation between Kinetic and Potential energy of an isolated multi-particle system.

Gravitational potential energy

Potential energy of a spring and block system

Potential energy curve.

Relation between interaction (force) and potential energy.

Equilibrium points

Conservative Force

Gravitational Force:

Throw (click play) a ball up with initial velocity and watch its kinetic energy in energy meter (red bar).

What happens to the kinetic energy of disk, when it goes up and when it comes back to its original position?

Spring Force:

Consider a block attached to a spring on a friction less surface.

Push the block (click play) towards left with initial velocity and watch its kinetic energy in energy meter (red bar).

When the block moves away from its zero position the spring force takes away its kinetic energy ( it does negative work on the block).

Work done by a Conservative Force is Path Independent

In the ball-earth or spring-block examples we have seen that .

In that case the net work done by gravitational force (spring force) on ball (block) in a round trip will be zero

The net work done by a conservative force on a particle moving around any closed path is zero.

An important result from above statement is

The work done by a conservative force on a particle moving between two points does not depend on the path taken by the particle.

Suppose a particle moves from point a to point b along either path 1 or path 2.

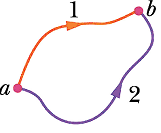
If only a conservative force acts on the particle, then the work done on the particle is the same along the two paths.

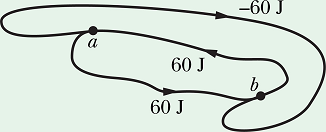
Checkpoint-1: Conservative force

The figure shows three paths connecting points a and b. A single force does the indicated work on a particle moving along each path in the indicated direction. On the basis of this information, is force conservative?

Example 1: Path Independence

A 60 kg skier starts from rest at height H=20 m above the end of a ski-jump ramp and leaves the ramp. Neglect the effects of air resistance and assume the ramp is frictionless.
How much work is done by the gravitational force from start to the end of ramp?

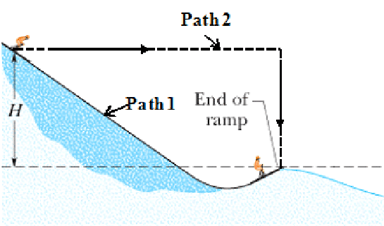
Key Idea: Work done by gravitational force (conservative force) is path independent.
Therefore work done in moving from start to end point through path-1 should be equal to work done from start to end point through path-2  

Non conservative force

Consider a block attached to a spring on a surface with friction.

Push the block (click play) towards left with initial velocity and watch its kinetic energy in energy meter (red bar).

How the kinetic energy changes with each round trip?

Single particle and Energy Principle

Consider a bouncing ball (single particle system) with Earth as the only surrounding.

Now throw the ball (click play).

The bouncing ball (system) moves under the influence of surrounding or external force (gravitational force)  .

As per energy principle "change in kinetic energy ΔK of a single particle system (ball) is equal to work done by net surrounding or external force".

Will this method work if we treat it as a multi-particle (ball + earth) system?

Multi-particle system

A multi-particle system comprises of at least two or more particles.

Now let us imagine that bouncing ball + earth is the system (enclosed in dashed blue line).

It is a simple two particle system.

No surrounding or external force is acting on the system , therefore

Now throw the ball.

The ball moves under the influence of gravitational force, which is now the internal force of the system .

Certainly kinetic energy of the ball still changes (ΔK≠0) under the influence of gravitational force.

However, there is a problem: The surrounding did no work on the system but ΔK≠0!

Potential Energy

Has Energy Principle been violated?

Answer to the question is a certain NO.

It only means that we have overlooked a kind of energy that is present in multi-particle systems.

This energy is associated with each pair of interacting particles inside the system.

This interacting energy of each pair is called "potential energy". Symbol U is used for potential energy.

Energy principle for a multi-particle system

Energy principle is same for a multi-particle system as it is for a single particle system.

Change in total energy of a system is equal to the work done by surrounding (or external forces).

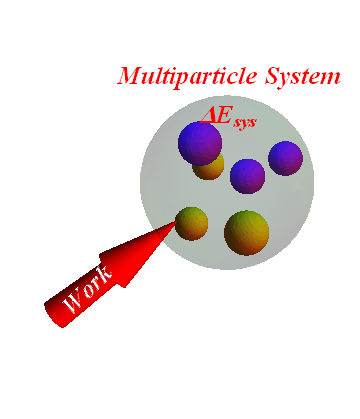
Total energy of a multi-particle (two or more particles) system is the sum of three parts.

Sum of rest energies of each particle.

Sum of kinetic energies of each particle.

Sum of potential energies of each pair of particles.

Sum of kinetic energy and potential energy of a system is also called it mechanical energy .

Change in total energy of a multi-particle system contains three parts.

Here Δu is the change in rest energy of the system (It will be zero as long as mass of each particle is not changing).

If mass of the system is constant or Δu=0.

Relation between ΔK and ΔU of an isolated multi-particle system

For an isolated multi-particle system, no work is done by surrounding , therefore is zero.

For such a system

Note: This is only true if rest energy or mass of the system is constant.

How to compute change in potential energy ΔU?

In multi-particle system, the change in potential energy of each pair (ΔU) is equal to the negative of the work done by internal force acting between the pair.

In bouncing ball-earth system, is the work done by gravitational force (internal force) acting between the ball and earth.

When the ball is raised to height h, the work done by -mg force will be

If is the initial potential energy on the ground surface and U is potential energy at height h, then

If we assume that initial potential energy of an object on the ground surface , then its potential energy at height h is

Example 2: Ball and Earth

A ball of mass 100 g is 2 m above the ground, headed upward at a speed of 15 m/s. The ball comes to a momentary stop at height of 5.27 m above the ground. Consider the ball + Earth as the system. (a) What is the change in potential energy of the system? (b) What is the change in kinetic energy of the system?

Solution:

Properties of Potential Energy

Potential energy depends on the separation between pairs of interacting particles, not on their individual positions.

Potential energy must approach zero as the separation between pairs of interacting particles becomes very large.

If an interaction is attractive (gravitation force), potential energy becomes negative as the distance between particles decreases.

If an interaction is repulsive (force between like charges), potential energy becomes positive as the distance between particles decreases.

Shape of any object or system depends on separation of different interacting particles of the object. When separation between interacting pairs change, shape of the object change.

Therefore we can say that when shape of a system changes, its potential energy changes. /p>

NNo potential energy exists between non interacting/span> pairs of particles.

Potential Energy in a Block - Spring System

CConsider a block-spring system. (Click, hold and drag the block to push or pull it from equilibrium position)

For such a system, spring force span> is an internal force.

Work done by this internal force in moving the object from to is

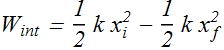
Change in potential energy of a two particle system is

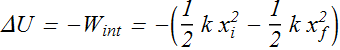
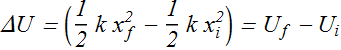
The potential energy U(x) of a spring-block system at a separation x from equilibrium position x=0 will be

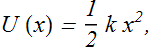
Potential Energy Curve

If we have a potential energy U(x) versus position x curve, we can gather a wealth of information about the motion of a particle.

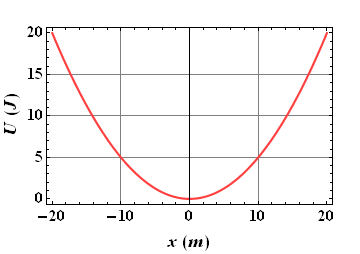
The first parameter that we can determine is the force using the potential energy versus position curve.

Relation between force and potential energy

For one - dimensional motion, the work done by an internal conservative force of a system is

Here Δx is the change in separation of two objects.

Now we can relate to its change in potential energy ΔU

The average force during this displacement can be given as

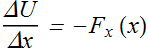
If we take the limit Δx→0, the force   at position x can be given as

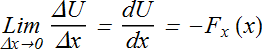
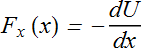
Force at any position is the negative of the slope of potential energy U(x) vs. position x curve.

Consider a U(x)) vs. x/em> curve

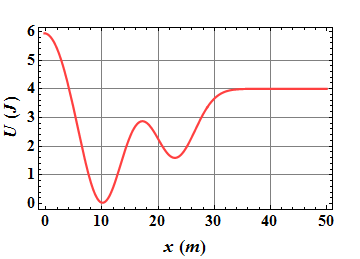
What is the slope of the curve at x=10m , x=17m, x=23m and x=40m ?

The  slope of UU(x) vs.  x/em>  curve at x=10m , x=17m, x=23m and x=40m is zero, thus at these positions.

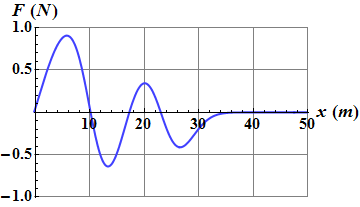
Is the slope dU/dx between  x/em>=0 and x=10m and between x=10m and x=17m is positive or negative?

How to predict motion of an object from its U(x) vs. x curve?

You can imagine as if the potential energy U(x) vs. x curve corresponds to a container of same shape.

Release (click play) disk (green) and watch the motion of the disc and its shadow (red disk) on x-axis.

Shape of a roller coaster too is same as shape of its potential energy vs. position curve.

Equilibrium Points

TThe positions where the slope  dU/dx=/span>0 and thus are called equilibrium points.

Neutral Equilibrium :

A region for which such as the region x > 35m  is called a region of neutral equilibrium.

If a particle has total mechanical energy , then its kinetic energy K=0 and the particle will be stationary at any point in this region.

Stable Equilibrium :

Minima in UU(x) vs. x/em> are position of stable equilibrium: Like a particle with   at position x=10m.

If we displace the particle either to left or right of x=10m the force will bring it back to x=10m.

Unstable Equilibrium :

Maxima in UU(x) vs. x are position of unstable equilibrium: Like a particle with   at position x=17m.

If we displace the particle either to left or right of x=17m the force will tend to take it further away from x=17m.

Work done by a non-conservative force

Consider a constant horizontal external force pulling a block along x axis through a displacement

Block's velocity increases from to

During the motion, a constant kinetic frictional force from the floor acts on the block.

Therefore net force acting on the block is given as

Total work W done by net force is equal to change in mechanical energy

In this situation there is no change in potential energy, therefore

Or

The work done by applied force will be

Work done by force of friction changes thermal energy of the system (Block and floor gets warmer)

Therefore

In a more general situation (say, block is moving up a ramp), there can be a change in potential energy. To include such a possible change, we write