Oscillations
Objectives
In this chapter we will learn about oscillations. After finishing this chapter we should know following topics:
What is a Simple Harmonic Motion (SHM)
Various terms used in SHM, like frequency, angular frequency, phase and time period
How velocity of an object performing simple harmonic motion is related to its displacement?
In simple harmonic motion, what is the relation between acceleration and displacement
What kinds of forces cause simple harmonic motion?
Linear Simple harmonic motion of a spring block system
How to measure spring constant of a spring
Energy of a simple harmonic oscillator
Angular simple harmonic motion
Angular speed of an angular simple harmonic oscillator
How to measure rotational inertia of a complicated shaped object
Simple pendulum and Physical pendulum
Damped harmonic oscillator
Forced oscillations/Resonance
What is Harmonic Motion?
Any motion that repeats itself at regular intervals is called periodic motion or harmonic motion.
Frequency:
Frequency is number of oscillations completed in one second. The symbol for frequency is f.
Units of Frequency :
SI unit of frequency ![]() and it is also called hertz (Hz).
and it is also called hertz (Hz).
![]()
Period (T):
Time period or period is the an oscillator takes to complete one cycle or one oscillation. Symbol for period is T. Frequency is related to T as
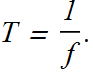
What will be SI units of Time period T?
Checkpoint-1: (Harmonic Motion)
A spring block system completes 25 oscillations in 10 s.
(a) What is its frequency f ?
(b) What is its period T ?
What is Simple Harmonic Motion?
Consider a rotating object with uniform angular velocity (frequency) ω.
Now watch the motion of its shadow on x-axis (Select shadow).
Motion of the projected image or shadow of a uniformly rotating object on xz-plane or yz-axis is called simple harmonic motion (SHM).
We (select show components) can see that at any instant of time, position ![]() of shadow is the x-component of the position vector
of shadow is the x-component of the position vector ![]() of rotating object.
of rotating object.
![]()
For the rotating object angular displacement θ(t) at any time t is
![]()
Where φ is starting angle at t = 0. By plugging the value of θ(t) we can write position vector components ![]() as a function of time.
as a function of time.
![]()
Any moving object whose displacement is represented by above function is said to be in simple harmonic motion (SHM).
Terms used in SHM
SHM is a sinusoidal function.
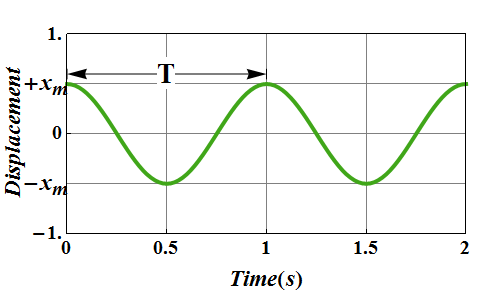
Displacement vs. Time plot of a simple harmonic motion is shown below.
Convention is to take cosine function to represent of SHM.
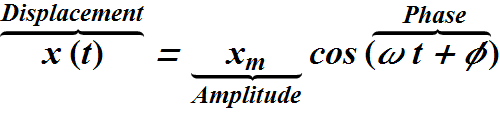
Phase is always measured in radians.
Different constant in phase term (ω t +φ) as follow
ω is angular frequency.
φ is initial phase or phase constant.
Angular frequency & Time Period
Definition of time period T is that it is the time an oscillator takes to complete one oscillation
Therefore after time T the displacement x(t) of the oscillator must return to its initial value.
Mathematically we can say displacement x(t) at time t, must be equal to displacement x(t+T) at time t+T.
![]()
This is only possible if
![]()
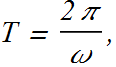
Checkpoint-2: SHM
An object undergoing simple harmonic motion at time t = 0 is at position ![]()
![]() is its amplitude) from its origin, (a) what is its initial phase φ?
is its amplitude) from its origin, (a) what is its initial phase φ?
If T is the time period, what will be the position of this object at
(b) t= 2.50T, (c) t= 3.00T, and (d) t= 5.25T
The Velocity of SHM
How to compute instantaneous velocity of an object in simple harmonic motion?
The velocity of a particle moving with simple harmonic motion can be obtained from derivative of its displacement.
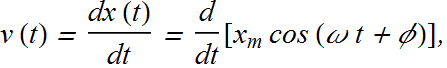
![]()
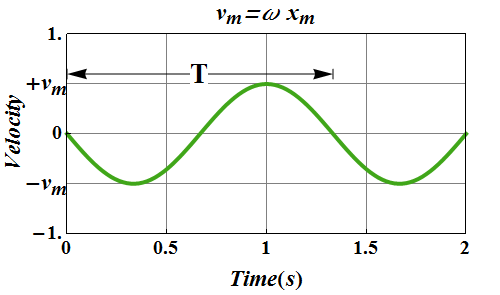
![]() is the maximum velocity magnitude and is called velocity amplitude.
is the maximum velocity magnitude and is called velocity amplitude.
The velocity of the particle varies between the limits ![]() .
.
The Acceleration of SHM
Once we know the velocity v(t) for a simple harmonic motion, we can find acceleration of the oscillating particle by again differentiating with time.
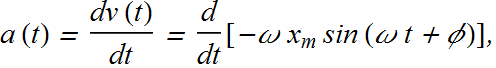
![]()
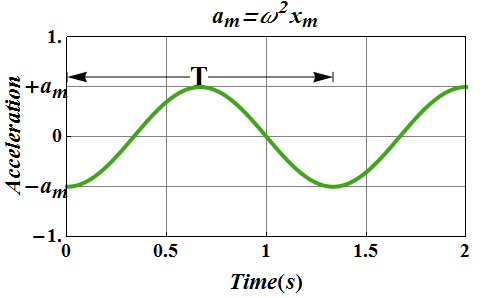
![]() is maximum magnitude of acceleration and is called the acceleration amplitude.
is maximum magnitude of acceleration and is called the acceleration amplitude.
The acceleration of the particle varies between the limits ![]() .
.
In the expression for acceleration, term ![]() is the expression for displacement x(t) of the oscillating object.
is the expression for displacement x(t) of the oscillating object.
Therefore, we can combine the expression for acceleration with that of displacement as:
![]()
This is the hallmark of simple harmonic motion:
Acceleration of any object in SHM, is always proportional to its displacement with opposite sign. Proportionality constant is equal to square of its angular frequency.
Checkpoint-3: SHM
Following are the relationships between the acceleration a of a particle and the particle’s position x. Which of these particles are performing simple harmonic oscillation?
(1) ![]() , (2) a = -4 x , (3)
, (2) a = -4 x , (3) ![]() , (4) a = 10 x
, (4) a = 10 x
What are the angular frequencies of the particles performing SHM?
Problem 1(SHM):
The position of a particle in simple harmonic motion is given as x(t)=10.0 cos(20.0t+2.00)
What is its velocity amplitude?
![]()
![]()
What is the amplitude of its acceleration?
![]()
What is its frequency f and time period T?

What is its phase at t = 0?
What kind of force can cause Simple Harmonic Motion?
Now we know
Acceleration of an object performing SHM, is always proportional to its displacement with a negative sign.
![]()
According to Newton’s second law the acceleration a of an object is related to the net applied force F on the object.
![]()
This means applied force capable of producing SHM, should be proportional to the displacement but opposite in sign.
![]()
The proportionality constant k is related to the angular frequency ω.
![]()
Any force acting on a particle that is proportional to the displacement of the particle with negative sign, will cause the particle to perform simple harmonic motion.
Checkpoint-4: SHM
Following are some forces related to the displacement x of a particle. Which of the forces will make the particle to perform SHM?
(a)![]() , (b) F = 10 x , (c)
, (b) F = 10 x , (c) ![]() , (d) F = -10 x?
, (d) F = -10 x?
Linear Simple Harmonic Oscillator
We know now that when an object experience a force that is proportional to the displacement of the object but opposite in sign, the object will undergo simple harmonic motion. In mathematical notation we can say
![]()
This relation is similar to Hook's law for a spring. That means the block spring system which follows this law, should form a linear simple harmonic oscillator.
As we have seen that the proportionality constant k is related to the angular frequency of the simple harmonic oscillator
![]()
The angular frequency and period for such a system can be given as
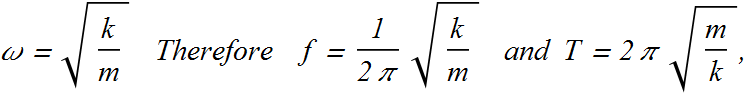
Can you answer?
If you are given a spring of unknown spring constant, can you suggest a method to measure its spring constant?
We have seen frequency and time period of a spring block system is given as
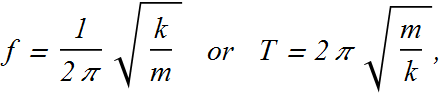
We can always measure frequency f or time period T of an oscillating object.
Once we know T and mass of the block, we can always compute spring constant k of the spring.
The frequency would double.
The frequency would be reduced to one-half its initial value.
The frequency would be reduced by a factor of (1/√2).
The frequency would increase by a factor of √2.
The frequency would be unchanged.
Energy in SHM
Potential energy of a system similar to a spring and mass system is given as.
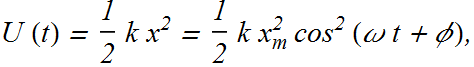
The kinetic energy is associated with its velocity.
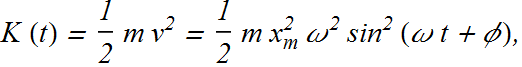
Since ![]() we can write K (t) as
we can write K (t) as
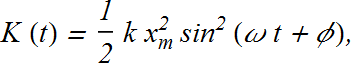
Variation of energy of a SHO with position from equilibrium
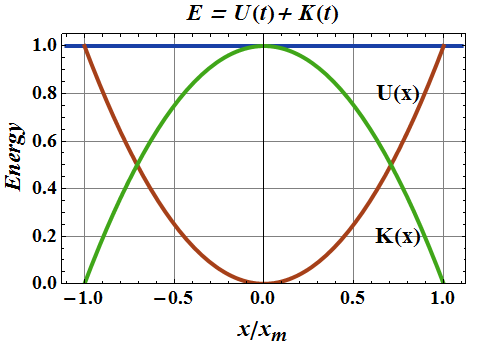
Now total energy of the system is
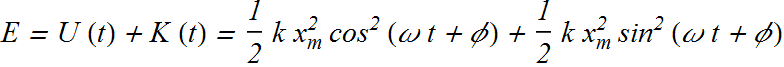
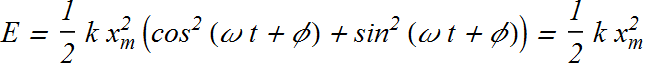
since
![]()
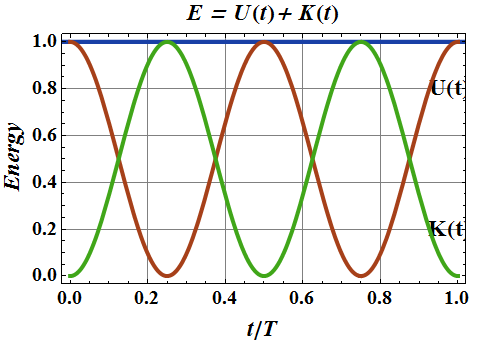
Variation of Energy of a SHO with time
Problem 3(Energy of a SHM):
An oscillating block–spring system has a mechanical energy of 1.00 J, an amplitude of 10.0 cm, and a maximum speed of 1.20 m/s.
Find the spring constant k.
Find the mass of the block.
Find the frequency of oscillation.
Angular Simple Harmonic Oscillator
Angular Simple harmonic motion is the motion executed by an object subject to a torque that is proportional to the angular displacement of the particle but opposite in sign.
![]()
Here κ (Kappa) is a constant, called the torsion constant.
![]()
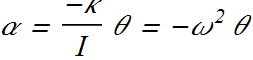
ω is not the angular speed here, it is angular frequency of the oscillator.
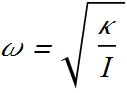
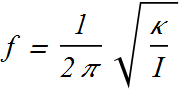
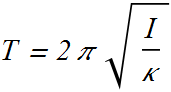
the disk
the rod
the sphere
The disk and the rod will oscillate with the same frequency.

What will be angular speed of an Angular Simple Harmonic Oscillator?
For an angular simple harmonic oscillator, angular displacement θ at any time is given as
![]()
Now the angular speed ϖ (Greek v)at any instant of time will be given as.
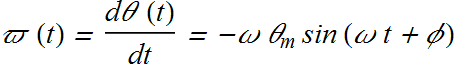
Similarly angular acceleration of an angular harmonic oscillator is given as.
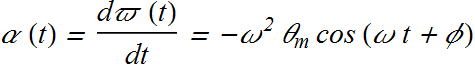
The angular speed ϖ and angular frequency ω are two different quantities.
Can you answer?
If you are given an odd shaped object, can you suggest a method to measure its rotational Inertia?
Problem 4(Angular SHM):
An odd shaped object of mass 95 kg is suspended by a vertical wire. A torque of 0.20 N·m is required to rotate the sphere through an angle of 0.85 rad and then maintain that orientation. When the object is released its period of oscillation T = 12 s.
What is the rotational inertia of the odd shaped object?
If the system can perform angular simple harmonic motion, the torque is related to angular displacement by following relation
![]()
The Simple Pendulum
Simple pendulum also performs SHM, let us see how?
Displace the pendulum from its equilibrium position by an angle θ.
Two forces are acting on a simple pendulum, Force ![]() due to gravity and force of tension T.
due to gravity and force of tension T.
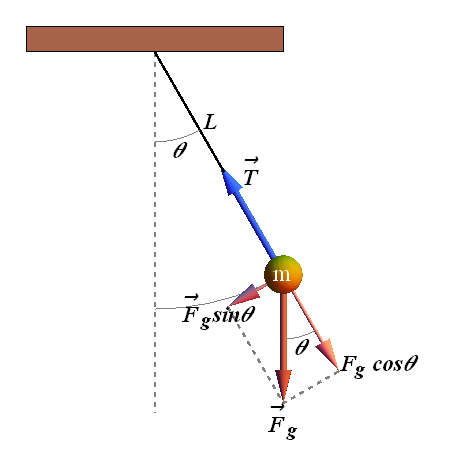
Total torque acting on a simple pendulum torque will be given as.
![]()
For a small value of angle θ
![]()
![]()
We can see torque τ acting on the object is proportional to angular displacement θ with negative sign, therefore this torque will produce simple harmonic motion.
If I is rotational inertia and α is its angular acceleration
![]()
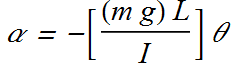
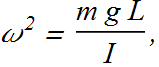
For simple pendulum ![]() , therefore the angular frequency of such a pendulum is
, therefore the angular frequency of such a pendulum is
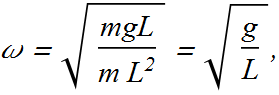
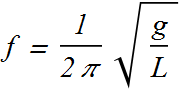
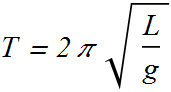
Frequency of simple pendulum is independent of its mass but changes with its length.
Let us watch how frequency of the pendulum changes if we change length of the cord or if we change mass of the ball?
The frequency would double.
The frequency would be reduced to one-half its initial value.
The frequency would be reduced by a factor of (![]() ).
).
The frequency would increase by a factor of ![]() .
.
The frequency would be unchanged.
What is a Physical Pendulum
When a rigid body is pivoted at any point away from its center of mass, it becomes a physical pendulum.
Examples: A Baseballs bat hanging from its handle or a hoop hanging on its rim.
A real pendulum, usually called a physical pendulum, can have a complicated distribution of mass.
Angular frequency of Physical Pendulum
Consider a physical pendulum, tilted by an angle θ from its equilibrium position.
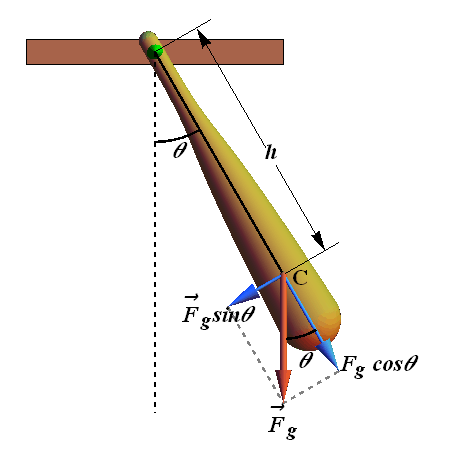
Total torque acting on the physical pendulum is due to force ![]() and is given as.
and is given as.
![]()
For a small value of angle θ
![]()
![]()
If I is rotational inertia and α is its angular acceleration
![]()
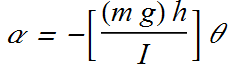
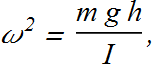
The angular frequency of such a pendulum is
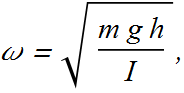
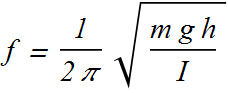
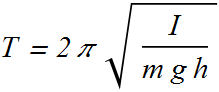
The clock will run slow.
The clock will run fast.
The clock will run the same as it did at sea level.
The clock cannot run at such high altitudes.
Checkpoint-5: Physical pendulum
Three physical pendulums, of masses ![]() ,
, ![]() , and
, and ![]() , have the same shape and size and are suspended at the same point.
, have the same shape and size and are suspended at the same point.
Rank the masses according to the periods of the pendulums, greatest first.
Damped Simple Harmonic Motion
Up till now we have considered the ideal conditions where no resistance (like friction or drag force) was present to the SHM.
In real life any object in simple harmonic motion will experience resistance due to force of friction or drag force from the medium (air or water etc.).
When the motion of an oscillator is reduced by an external force, the oscillator and its motion are said to be damped.
When the damped force ![]() is a drag force from water, air or any fluid, it is proportional to the velocity of the object.
is a drag force from water, air or any fluid, it is proportional to the velocity of the object.
![]()
If we consider a system as shown in figure, the net force ![]() acting on the block will be
acting on the block will be
![]()
This should be equal to the acceleration of the block
![]()
I about any other axis is given as
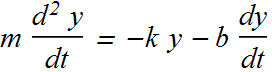
The solution of this differential equation is
![]()
![]()
With angular frequency
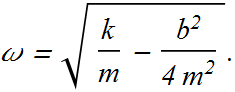
Checkpoint-6: Damped Oscillations
Here are three sets of values for the spring constant, damping constant, and mass for the damped oscillator of the above figure.
Rank the sets according to the time required for the mechanical energy to decrease to one-fourth of its initial value, greatest first.
| Set 1 | |||
| Set 2 | |||
| Set 3 |
Key Idea : Energy stored in the spring oscillating spring block system is
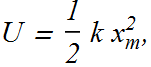
It means when amplitude ![]() becomes half, energy reduces to one fourth.
becomes half, energy reduces to one fourth.
If t is the time it takes to reduce the amplitude to one half of its original value
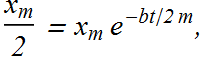
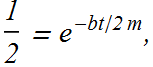
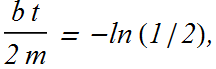
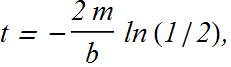
t is independent of k
Forced Oscillations and Resonance
When we apply a one-time push or force to a pendulum and let it oscillate, the pendulum will oscillate with its natural angular frequency ω.
If we apply a continuously oscillating force ![]() (simple harmonic force) of angular frequency
(simple harmonic force) of angular frequency ![]() , the pendulum will oscillate with angular frequency
, the pendulum will oscillate with angular frequency ![]() .
.
![]()
The amplitude ![]() of such force oscillation will depend upon how much positive work the applied force can do on the pendulum.
of such force oscillation will depend upon how much positive work the applied force can do on the pendulum.
Work done by any force is given by
![]()
Work done will be maximum, if the force ![]() and displacement x are always in same direction.
and displacement x are always in same direction.
That is only possible if the applied force is oscillating in phase with the natural oscillation of the pendulum.
In other words when ![]() . Such a condition is called resonance.
. Such a condition is called resonance.

