Measurements
Objectives
In this chapter we will review the following concepts:
Measurement of a physical parameter
Units, Systems of units
Basic Units in Mechanics
Changing units
Significant figures
Writing very large and very small numbers
Dimensional Analysis
Measurements
Why we measure?
Suppose you want to compare the length of your lawn with its width: You need to measure the length and width of the lawn.
You want to know whose weight is more, yours or your friend's: You need to measure your mass and your friend's mass.
You want to know whose pulse is faster, yours or your friend's: You need to measure time.
How we measure?
We measure parameter (length in this case) of any object by comparing it same parameter (length) of an other object.
For comparison of length and width of your lawn what you need?
We need an other object say a piece of a tape (need not be a measuring tape) or a stick (it could be a meter stick but not necessary).
Now we compare (measure) the length and width of the lawn with the length of the tape or stick and present our results as
Lawn length is "30 times of the tape length"
Lawn width is "20 time of the tape length"
Units of measurement
In above measurement example, the "tape length" is called the unit of measurement.
If we would have used a meter stick: The "meter stick length" would have been called unit of measurement.
For any kind of measurement we need a "unit of measurement and measurement of a parameter (length, mass, time --) is comparison of that parameter with corresponding unit of measurement".
The International System of Units
If you want to communicate about your measurements with others in the world, you can not use any random piece of tape or random stick (random unit) for length measurement.
You need to agree upon some Standard Units of measurements.
Following are some examples of different systems of Standard Units.
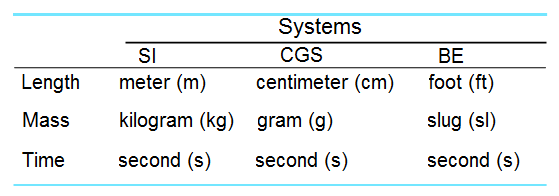
Note: SI Units used to be called MKS system of units.
In this course we will use International system of units (SI or Système International). It is also known as metric system.
How to write measured values?
When we measure (or compare) the length of an object with a standard unit say meter (m), the result can be written as
The length of the object is "20.5 times the length of the meter (m)"
In short hand we just write, the length of the object is "20.5 m"
Similarly if we measure (or compare) the mass of an object with a standard unit say kilogram (kg), the result can be written as
The mass of the object is "5.5 times the mass of the kilogram (kg)"
In short hand we just write, the mass of the object is "5.5 kg"
Does this mean that we have to define units for all parameters?
The answer is no. In mechanics we need to define units only for three parameters:
Length, Mass and Time, units for these parameters are regarded as base units. (SI base units are m, kg, and s)
How we measure the other parameters?
Units for other parameters are defined in terms of these base units and are called derived units.
For example unit for measuring speed is defined in terms of length and time. SI units for speed is m/s.
Length
Unit of length: “Meter” was originally defined in terms of the distance measured along the earth’s surface between North pole (point A) and Equator (Point B).
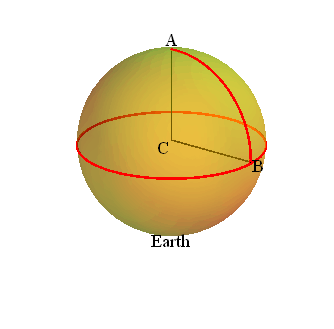
1 meter ≡ AB/10 000000
Eventually, a more accurate standard was needed, and by international agreement the meter became the distance between two marks on a bar of platinum-iridium alloy kept at 0 °C.

Today meter is defined as the distance traveled by light in vacuum during a time interval of 1/299 792 458 of a second.
This definition arises because the speed of light is a universal constant and is defined to be 299 792 458 m/s.
Mass
Originally, the kilogram was expressed in terms of a specific amount of water (One liter).

Today one kilogram is defined to be the mass of a standard cylinder of platinum-iridium alloy, kept at the international Bureau of weights and measures in Sèvres, France
A Second Mass Standard:
It is the carbon-12 atom, which, by international agreement, has been assigned a mass of 12 atomic mass units.
![]()
Time
Unit of time: “second” was originally defined as average time for the earth to rotate once about its axis (mean solar day), divided by 86 400.
1 day = 24 × 60 × 60 = 86 400 seconds
There is a problem with this definition?
The length of the day is not constant
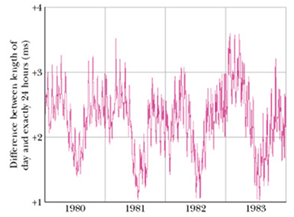
Today we still use a naturally occurring repetitive phenomenon to define a second, but a very different one.
Second is derived from electromagnetic waves emitted by cesium-133 atoms in an atomic clock.
One second is the time taken by 9192631770 oscillations of the light (of a specified wavelength) emitted by a cesium - 133 atom.
Significant Figures
The significant figures (also called significant digits) of a number are those digits that contribute to its precision.
Significant figures (significant digits) includes all digits except :
leading zeros where they serve merely as placeholders to indicate the scale of the number.
trailing zeros in a number not containing a decimal point.
Example 1: 00407 has three significant figures (digits) : 4, 0 and 7. Leading zeros are not counted. Zeros appearing anywhere between two non-zero digits (there is a zero between 4 and 7) are significant.
Example 2: 0.00035 has two significant figures (digits) : 3 and 5. Leading zeros are not counted.
Example 3: 43500 has three significant figures (digits) : 4, 3 and 5. Trailing zeros are not counted in the absence of decimal point.
Example 4: 50000 has only one significant figure (digit) : 5. Trailing zeros are not counted in the absence of decimal point.
Example 5: 5.1000 has five significant figures (digits) : 5, 1, 0, 0 and 0. Trailing zeros are counted in the presence of decimal point.
Example 6: 0.00372000 has six significant figures (digits) : 3, 7, 2, 0, 0 and 0. Leading zeros are not counted but trailing zeros are counted in the presence of decimal point.
Scientific notation
Same rules apply to numbers expressed in scientific notation.
In scientific notation, placeholder leading and trailing digits do not occur, so all digits are significant.
Scientific notation is used to express the very large and very small quantities.
Example 1: 0.00035 (two significant digits) becomes ![]()
Example 2: 0.000325400 (six significant digits) becomes ![]() .
.
Example 3: 2500 (two significant digits) becomes ![]() .
.
Example 4: 3560 000 000 (three significant digits) becomes ![]() .
.
Standard prefix for SI Units
Attaching a prefix to an SI unit has the effect of multiplying with the associated factor.

Example 1: ![]()
Example 2: ![]()
Measurements & Significant Figures
The significant figures (significant digits) in a measured value depends on the precision of the measuring instrument.
Let us measure length L of an object with a standard (30 cm long) ruler with smallest division of 1 mm.
Suppose the measured length is little greater than 0.123m and less than 0.124 m.
It would be meaningless to write length as: L=0.1234 m, because the ruler can not measure a fraction of a millimeter.
Means with a standard (30 cm long) ruler with smallest division of 1 mm, length can be measured up to three significant figures with an accuracy of 1 mm.
![]()
 |
| Ruler |
Suppose now the same object is measured with a caliper with an accuracy of 0.1 mm. The measured length can be written as L=0.1234 m.
So we can say, with a caliper we can measure up to four significant figures with an accuracy of 0.1 mm.
![]()
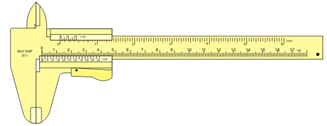 |
| Caliper |
Rule for significant figures in calculations
In a calculation the number of significant figures in the final answer should be rounded to the smallest number of the significant figures of the used parameters in the calculations
Example 1: A car traveling with constant speed covers a distance d = 123 m in a time t = 7.89 s. Calculate speed of the car.
The speed v is

It is meaningless to use 9 significant figures.
Used parameters are d and t which are known with an accuracy of only three significant figures, therefore v can only be expressed up to three significant figures.
Value of v should be rounded to three significant figures.
![]()
Example 2: Calculate the area A of a garden with sides of W=9.8 m and L=17.1 m.
Area A of the garden is computed as
![]()
It is meaningless to use 5 significant figures.
Used parameter is L known with an accuracy of only three significant figures and W is known with an accuracy of only two significant figures, therefore lowest accuracy used is two significant figures.
Value of A should be rounded to two significant figures.
![]()
Dimensions
In physics, the term dimension is used to refer to the physical nature of a quantity.
Fundamental dimensions in mechanics are length [L], time [T], and mass [M].
Each dimension can have different units:
Dimension length [L] can have units like meters (m), miles or foot (ft).
Dimension time [T] can have units like hour (hr), second (s) or year.
Dimension mass [M] can have units like kilogram (kg), slug (sl) or gram (g).
Each unit can refer to only one dimension:
Unit meter (m) corresponds to dimension length [L] only.
Unit second (s) corresponds to dimension time [T] only.
Unit kilogram (kg) corresponds to dimension mass [M] only.
Changing Units
Since any dimension can have more than one units, therefore we often need to change units.
Generally it is done by multiplying original measurement by a conversion factor.
Such a conversion method is called chain Link method:
Example of conversion factor:
Convert express highway speed of 65 miles per hour in meters per second.
First find out relation between 1 mile and meter & between hour and second..
1 mile = 1609 m; Therefore conversion factor is
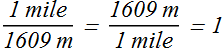
1 hour = 3600 s; Therefore conversion factor is
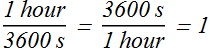
Use the appropriate conversion factor to replace the unit with new unit.
For replacing unit "mile with unit m" (meter) we use conversion factor 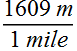 .
.
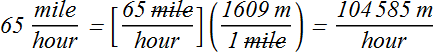
For replacing unit "hour with unit s" (second) we use conversion factor 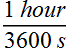 .
.
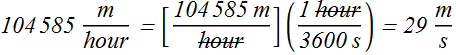
Therefore the answer is
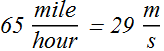
Dimensional Analysis
Dimensional analysis can be used to verify if a formula is correct or not.
Suppose we wish to calculate the distance d traveled by a car, but we are not sure whether the correct formula is
![]()
Or

We can check the dimensions on both side of equal sign.
If left hand side dimensions are not equal to dimension on right hand side the relation is certainly incorrect.
If left hand side dimensions are equal to dimension on right hand side, we can only say that the relation is dimensionally correct but we can not say if the relation will give correct magnitude.
Let us check first formula for speed
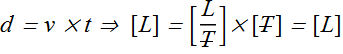
We see that dimension of left hand side is length [L] and dimension on right hand side is also length [L], therefore formula is dimensionally correct.
Let us check second formula for speed
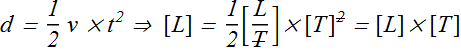
We see that dimension of left hand side is length [L] while dimension on right hand side is [L]×[T], therefore formula is certainly incorrect.
One of the necessary condition for a formula to be correct is: left hand side unit should be equal to the right hand side unit.
Summary
Science and engineering are based on measurements and comparison.
Each parameter is measured by comparison with a Unit.
We need to setup standard units for basic parameters (length, mass and time).
Standard Units for other parameters are derived from basic Units.
After setting up a standard units, we need procedures to measure.
“Measurement of the radius of hydrogen atom will require different procedure than the measurement of radius of sun.”
Significant figures of a measured value will depend on the precision of the measuring instrument.
Number of significant figures in the final answer should be rounded to the smallest number of the significant figures of the used parameters in the calculations.
One of the necessary condition for a formula to be correct is: left hand side unit should be equal to the right hand side unit.
