Magnetic Field
Objectives
In this chapter we will learn
How the magnetic Field is produced?
The definition of Magnetic field.
Motion of a charged particle in magnetic field.
Hall effect.
Cyclotron particle accelerator.
Magnetic force on a current-carrying wire.
Magnetic torque on a wire loop.
Magnetic dipole, magnetic dipole moment.
Electric Motor.
Permanent magnets and magnetic force.
We are familiar with the magnet, we use to hang notes on a refrigerator.
Compass needle is a permanent magnet on a low - friction pivot.
We know when a permanent magnet is brought close to iron nails, it attracts them (exert force on the iron nails).
When a permanent magnet is brought close to the compass needle, it also experience a force.
This force is not electric force but is called magnetic force.
How we know that it is not simply an electrostatic force?
Magnet is made up of neutral iron or steel and compass needle is also made up of neutral iron or steel.
There exists no electrostatic force between two neutral objects.
Compass needle also points toward Earth's magnetic north pole, while neither a charged object nor an electric dipole do this.
These observations clearly indicates that magnetic force is not electrostatic force.
How the magnetic Force is produced?
A stationary point charge generates an electric field given by
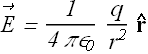
Move the charge (click play)
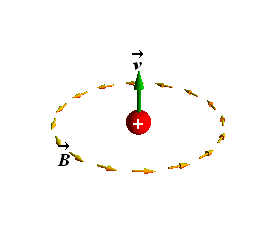
A moving charge not only produce an electric field ![]() but also a Magnetic field
but also a Magnetic field ![]()
A Magnetic field ![]() curls around the moving charge.
curls around the moving charge.
 |
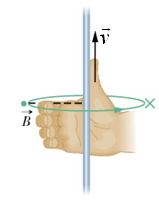 |
According to right hand rule if thumb points to the direction of motion of a charge, curled fingers point to the direction of magnetic field ![]() .
.
Biot - Savart Law
"Biot-Savart" is pronounced as bee-oh sah-VAR.
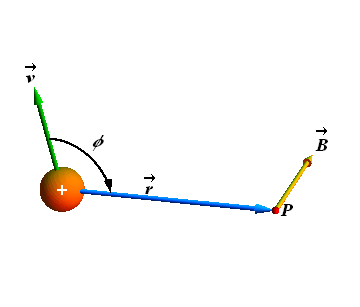
According to this law the magnetic field ![]() at a position
at a position ![]() due to a charge q, moving with velocity
due to a charge q, moving with velocity ![]() is given as
is given as
![]()
Where the value of constant ![]() is
is
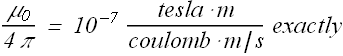
![]() is called permeability constant.
is called permeability constant.
Since the magnetic field ![]() is proportional to the cross product (×) of vector
is proportional to the cross product (×) of vector ![]() and
and ![]() , therefore the direction of
, therefore the direction of ![]() will always be perpendicular to
will always be perpendicular to ![]() and
and ![]() .
.
Two moving point charges not only exert electric force on each other but also exert a magnetic force on each other.
For the presence of magnetic force, both the charges should be in motion with respect to each other.
Magnetic force and definition of ![]()
If ![]() is the magnetic field at a point due to some moving charge (charges), the magnetic force
is the magnetic field at a point due to some moving charge (charges), the magnetic force ![]() on an other charge q at that point moving with velocity
on an other charge q at that point moving with velocity ![]() is given as
is given as
![]()
The magnitude of the force can be written as
![]()
where φ is the angle between velocity vector ![]() and magnetic field
and magnetic field ![]() .
.
In other words magnetic field is related to the magnetic force as
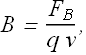
Magnetic field is the "force per unit positive charge per unit velocity".
SI units for magnetic field are Tesla.
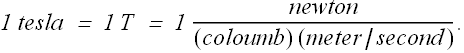
Or
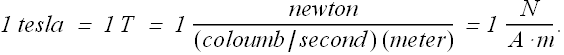
Direction of Magnetic Force
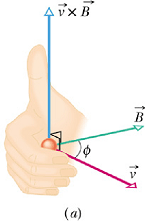 |
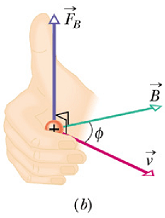 |
The direction of the magnetic force ![]() is given by the right hand rule as shown in the above figure (a) and (b).
is given by the right hand rule as shown in the above figure (a) and (b).
When q is negative the direction of ![]() will be opposite to that of
will be opposite to that of ![]() (figure c).
(figure c).
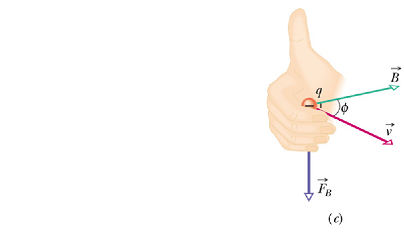
The force ![]() acting on a charged particle moving with velocity
acting on a charged particle moving with velocity ![]() through a magnetic field
through a magnetic field ![]() is always perpendicular to
is always perpendicular to ![]() and
and ![]() .
.
Since ![]() is always perpendicular to
is always perpendicular to ![]() therefore it can not change the magnitude of
therefore it can not change the magnitude of ![]() , it can only change the direction of
, it can only change the direction of ![]() .
.
Interactive Checkpoint - 1 (Direction of Magnetic Force)
A proton moving from south to north enters a uniform magnetic field ![]() directed into the page.
directed into the page.
(a) What will be the direction of magnetic Force ![]() ?
?
(b) If an electron replaces the proton, what will be the direction of magnetic Force ![]() ?
?
(c) What happens to ![]() for the proton if the magnetic field
for the proton if the magnetic field ![]() points out of the page?
points out of the page?
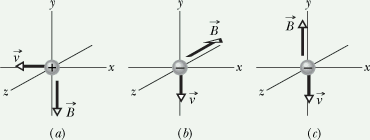
Checkpoint 1
The figure shows three situations in which a charged particle with velocity ![]() travels through a uniform magnetic field
travels through a uniform magnetic field ![]() . In each situation, what is the direction of the magnetic force
. In each situation, what is the direction of the magnetic force ![]() on the particle?
on the particle?
Magnetic Field Lines
Magnetic field lines are similar to electric field lines.
The direction of the tangent of a magnetic field line at any point gives the direction of ![]() at that point.
at that point.
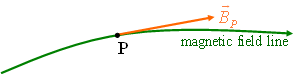
The spacing of the lines represent the magnitude of ![]() . Magnitude of
. Magnitude of ![]() at point P is more that at point Q.
at point P is more that at point Q.
Magnets are called magnetic dipoles, one pole is called north pole and other is called south pole.
The field lines of a magnet always enters the south pole, pass through the body of the magnet and leave through the north pole.
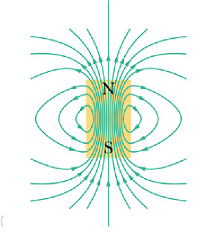 |
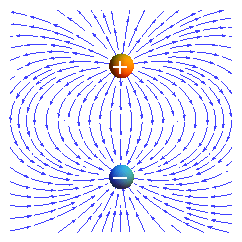 |
| Magnetic dipole | Electric dipole |
Contrary to field lines of an electric dipole, inside the magnet, field lines move from south to north pole.
Opposite magnetic poles attract each other, and like magnetic poles repel each other.
Magnetic monopole
There is a dramatic difference between the electric and magnetic dipoles.
The electric dipole is made of individual negative and positive charges ("monopoles") and can be separated from each other.
One might expect a magnetic dipole to be made of positive (north) and negative (south) magnetic monopoles, but no one has ever found an individual magnetic monopole.
When you cut a magnet in two, you do not get two magnetic monopoles, you just get two magnets.
Motion of a charged particle in magnetic field.
The Magnetic force ![]() on the charged (q) particle moving with velocity
on the charged (q) particle moving with velocity ![]() in magnetic field
in magnetic field ![]() is given as
is given as
![]()
![]()
This force is always perpendicular to the velocity of the particle like a centripetal force, therefore charged particle moves in a circular path and φ=90°.
As per Newton's second law, the magnitude of centripetal acceleration a is given as
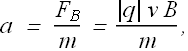
Where m is the mass of the charged particle.
In circular motion speed v of the charged particle is related to its centripetal acceleration.
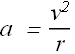
where r is the radius of the circular path.
Equating above two values of acceleration a gives us radius of the circular path of the charged particle.
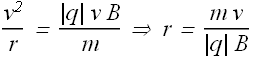
Radius decreases with increase in charge or magnetic field.
Radius increases with velocity or mass of the particle.
Now the time period T (the time to complete one revolution) is equal to the circumference divided by the speed:
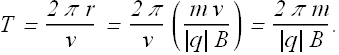
The frequency (number of revolutions per second) will be given as
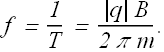
Angular frequency ω of the motion is given as
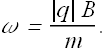
Interactive Checkpoint - 2 (Motion of charged particle in Magnetic field)
A positron (positive charged particle with same mass as electron) moving horizontally from south to north enters a uniform magnetic field ![]() directed out of the page.
directed out of the page.
(a) Will the positron moves in clockwise or anti-clockwise circular path?
(b) What happens to the radius if we increase the speed of the particle?
(c) What happens to the radius if we increase the magnitude of the magnetic field ![]() ?
?
(d) Will the radius change if we change it to an electron?
Interactive Checkpoint - 3 (Motion of charged particle in Magnetic field)
Two charged particles (one negative and other positive) of same speed v, moving horizontal from south to north enters a uniform magnetic field ![]() directed out of the page.
directed out of the page.
(a) If the mass of the negative charge particle is half of the positive particle which particle will have larger radius and how much?
(b) Which particle will have more number of revolutions per second and by what factor?
Helical Path
We have seen when velocity of a charge particle is perpendicular to the magnetic field it moves in a circular path.
What happens if angle is 0°?
What happens if angle 0°<φ<90°?
Perpendicular velocity component will cause a circular motion while parallel component will cause a linear motion, therefor the resulting path will be a helical path.
Watch how the pitch of the helix changes with angle θ between ![]() and
and ![]() ?
?
Aurora borealis in northern hemisphere can be explained by this phenomenon.
Crossed Fields
When electric field ![]() and magnetic field
and magnetic field ![]() are perpendicular to each other, they are called crossed fields.
are perpendicular to each other, they are called crossed fields.
Discovery of Electron
Let us see what happens when a charged particle moves in a crossed fields. We will do simulation of J. J. Thompson experiment.
When a negative charge (electron) moves through the plates with only electric field on, it experience a upward force.
When a negative charge (electron) moves through the plates with only magnetic field on, it experience a downward force.
With crossed fields on (both magnetic field and electric field on), we can adjust the magnitude of ![]() and
and ![]() in such a way that the net force on the charged particle is zero.
in such a way that the net force on the charged particle is zero.
If v is the velocity of the charged particle, when it enters the crossed fields with net force is zero, we can say
![]()
Or the magnitudes of both the forces should be same
![]()
Or
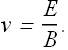
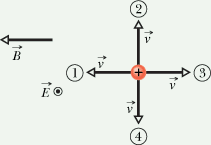
Checkpoint - 3 (Crossed Fields)
The figure shows four directions for the velocity vector ![]() of a positively charged particle moving through a uniform electric field
of a positively charged particle moving through a uniform electric field ![]() (directed out of the page and represented with an encircled dot) and a uniform magnetic field
(directed out of the page and represented with an encircled dot) and a uniform magnetic field ![]() . (a) Rank directions 1, 2, 3 and 4 according to the magnitude of the net force on the particle, greatest first. (b) Of all four directions, which might result in a net force of zero?
. (a) Rank directions 1, 2, 3 and 4 according to the magnitude of the net force on the particle, greatest first. (b) Of all four directions, which might result in a net force of zero?
Hall Effect
In 1879, Edwin H.Hall, then a 24 - year - old graduate student at the Johns Hopkins University, showed that the charges moving inside a conductor can also be deflected by a magnetic field.
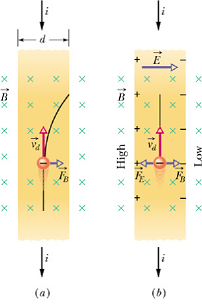
Consider copper strip of width d, carrying a current i. whose conventional direction is from the top of the figure to the bottom.
Let us apply an external magnetic field ![]() , pointing into the plane of the figure.
, pointing into the plane of the figure.
 |
 |
Each drifting electron in the strip will experience a magnetic force ![]() towards right hand side (figure a ).
towards right hand side (figure a ).
If ![]() is the drift velocity of the electrons, the magnetic force will be given as
is the drift velocity of the electrons, the magnetic force will be given as
![]()
Presence of magnetic deflection causes accumulation of electrons on the right hand edge of the strip.
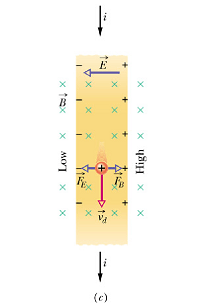
This accumulation will develop a potential difference V between the right and left edge (figure b).
This is called Hall potential difference V, and will generate an electric field E such that
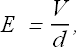
This electric field will try to deflects the electrons toward left hand side.
Electric force will appose the magnetic force.
When both these forces are equal, no further deflection will take place.
![]()
Drift velocity ![]() is related to the current density J and number density n of free electrons in a conductor.
is related to the current density J and number density n of free electrons in a conductor.
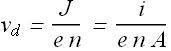
where A is the cross sectional area of the strip. By substituting the value of ![]() in balancing equation we get
in balancing equation we get
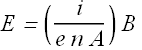
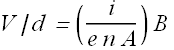
From this equation we can get the free electron density in a conductor.
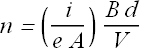
If ℓ is the thickness of the strip, A = ℓd. In terms of thickness n can be re written as
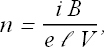
Hall effect can be used to measure free charge density n in a conductor and drift velocity ![]()
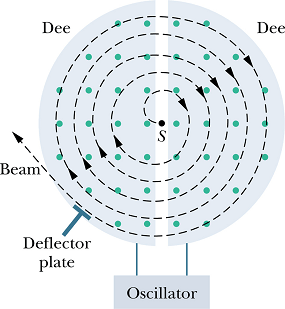
Cyclotron particle accelerator.
High - energy particles, such as high - electrons and protons, have been extremely useful in probing atoms and nuclei to reveal the fundamental structure of matter.
Cyclotron is one kind of particle accelerator.
A cyclotron accelerator consists of two hollow D-shaped conductors (copper) in which the particles (protons, say) circulate.
A uniform magnetic field is applied out of the page. And an alternating electric potential difference is applied to these D,s.
Electric field will alternate between the gap of these D,s. The alternating frequency is synchronous to the circulating frequency decided by the applied magnetic field. This is called resonance condition.
This field will increase the speed of the particle when ever it enters from one D to other.
The particle will go in a spiral path with increasing speed or increasing kinetic energy.
Finally it exits out from the cyclotron using an other deflecting electric field at the exit.
Magnetic force on a current-carrying wire.
A charged particle moving in a uniform magnetic field experience magnetic force.
It does not matter if it is moving in a free space or a conductor.
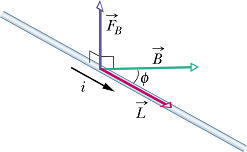
Consider a wire segment of length L carrying current i, placed in a uniform magnetic field ![]() coming out of the page.
coming out of the page.
Let the charges move (click play).
Suppose all the conduction electrons in segment L (blue) take time t to cross the line A.
If ![]() is the drift velocity then
is the drift velocity then
![]()
 |
Total charges crossing plane A in time t is given as
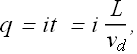
Magnetic force ![]() experienced by charges in segment L will be given as
experienced by charges in segment L will be given as
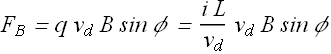
Or
![]()
In vector form magnetic force can be written as
![]()
Here ![]() is length vector that has magnitude L and is directed along the direction of current.
is length vector that has magnitude L and is directed along the direction of current.
Magnetic force on a current-carrying wire of arbitrary shape placed in Uniform Magnetic field
If the wire is not straight or the magnetic field is not uniform, we can imagine the wire broken up in small straight segments of length ![]() .
.
Magnetic force ![]() on each segment will be given as
on each segment will be given as
![]()
Net magnetic force ![]() on the whole wire is then the vector some of all these forces.
on the whole wire is then the vector some of all these forces.
![]()
Checkpoint 2
The figure shows a current i through a wire in a uniform magnetic field ![]() , as well as the magnetic force
, as well as the magnetic force ![]() acting on the wire. The field is oriented so that the force is maximum. In what direction is the field?
acting on the wire. The field is oriented so that the force is maximum. In what direction is the field?
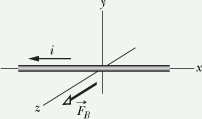
Hint: ![]() .
.
Interactive Checkpoint - 4 (Magnetic force on a current carrying wire)
A current carrying wire is placed in a uniform magnetic field ![]() .
.
(a) What will be the direction of force if current is pointing to the left and ![]() is pointing out of the page?
is pointing out of the page?
(b) What will be the magnetic force direction if current is switched to right?
(c) Will the force increase or decrease with increase in current?
A current carrying wire loop in a uniform magnetic field
Consider a rectangular wire loop of side lengths a and b carrying current i in a uniform magnetic field.
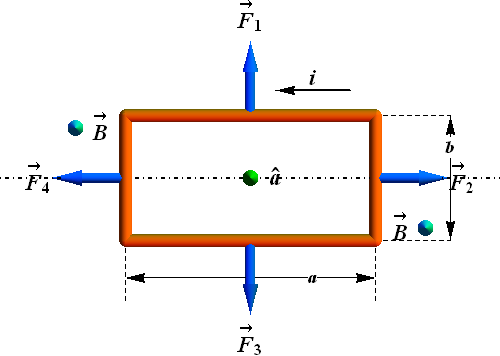
Will the loop be in equilibrium?
Net magnetic force on the wire loop.
Magnetic forces ![]() and
and ![]() experienced by the four sides of the loop are given as
experienced by the four sides of the loop are given as
![]()
And
![]()
If we add all the four forces, net force ![]() on the loop will be zero.
on the loop will be zero.
![]()
Net torque on the wire loop.
Let us now look at the net torque ![]() on the loop due to these forces.
on the loop due to these forces.
Let us tilt the loop such that loop area vector ![]() makes an angle θ with the magnetic field
makes an angle θ with the magnetic field ![]() .
.
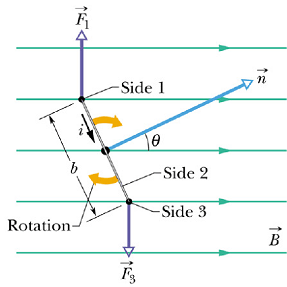
For force ![]() and
and ![]() the normal distance from the axis is zero as both the forces are acting along the axis. Therefore there is no torque due to these two forces.
the normal distance from the axis is zero as both the forces are acting along the axis. Therefore there is no torque due to these two forces.
Length vector ![]() and
and ![]() of side 1 and side 3 is always perpendicular to the magnetic field, therefore the magnitude of both the forces are given as
of side 1 and side 3 is always perpendicular to the magnetic field, therefore the magnitude of both the forces are given as
![]()
For force ![]() and
and ![]() the normal distance from the axis of rotation is
the normal distance from the axis of rotation is 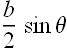 . Magnitude of torque
. Magnitude of torque ![]() due to this force will
due to this force will
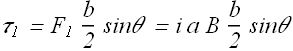
Similarly the magnitude of torque ![]() will be given as
will be given as
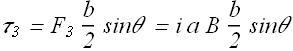
Both these torques will try to rotate the loop in clockwise direction, therefore the magnitude of net torque ![]() will be given as
will be given as

Product a b = A, area of the loop so above equation can be rewritten as
![]()
If there are N numbers of loops, total torque τ will be given as.
![]()
Although the formula is derived for a rectangular loop but it is true for any shape of loop.
Magnetic dipole & magnetic dipole moment.
We know that, when an electric dipole of dipole moment ![]() is placed in an electric field
is placed in an electric field ![]() it experienced a torque
it experienced a torque ![]() given as.
given as.
![]()
In vector form it is written as
![]()
θ is the angle between the dipole moment ![]() and electric field
and electric field ![]() .
.
Similarly when a current carrying loop is placed in a uniform magnetic field, it also experience a torque.
By same analogy we can call a current carrying coil a magnetic dipole of magnetic dipole moment ![]() .
.
The direction of the dipole moment is taken to be the direction of area vector ![]() . Torque
. Torque ![]() on a magnetic dipole can be written as
on a magnetic dipole can be written as
![]()
where θ is the angle between ![]() and
and ![]() . In vector form it can be written as
. In vector form it can be written as
![]()
Magnitude of μ is
![]()
According to right hand rule if the curled fingers point in the direction of current, thumb points in the direction of magnetic dipole moment ![]() .
.
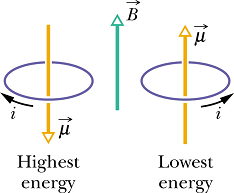
Potential energy of a magnetic dipole
When a magnetic dipole is placed in an external magnetic field, it has a magnetic potential energy.
![]()
θ is the angle between ![]() and the magnetic field
and the magnetic field ![]() .
.
A magnetic dipole has its lowest energy when it is parallel to the magnetic field ![]() .
.
A magnetic dipole has its highest energy when it is anti parallel to the magnetic field ![]() .
.
When an external torque rotates a dipole placed in a magnetic field from one position to other and dipole is stationary before and after the move, the work ![]() done by the applied torque will be given as
done by the applied torque will be given as
![]()
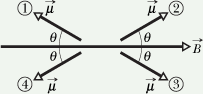
Checkpoint - 3 (Magnetic Dipole moment)
The figure shows four orientations, at angle θ, of a magnetic dipole moment ![]() in a magnetic field. Rank the orientations according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the dipole, greatest first.
in a magnetic field. Rank the orientations according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the dipole, greatest first.
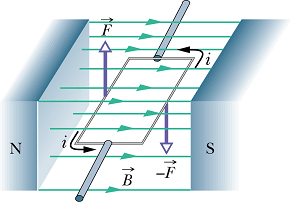
Electric Motor.
Electric motor is one of the most important instrument in this world. Following figure show a simple electric motor.
It consists of a rectangular wire loop carrying current i, placed in a uniform magnetic field ![]() .
.
A DC Electric Motor
