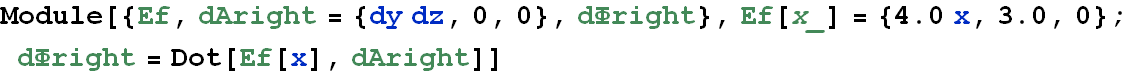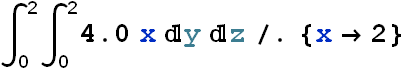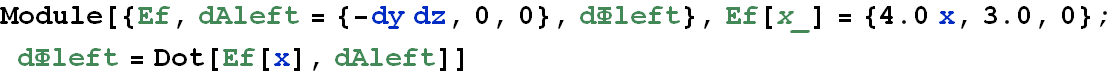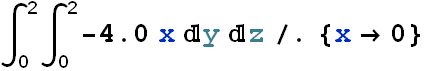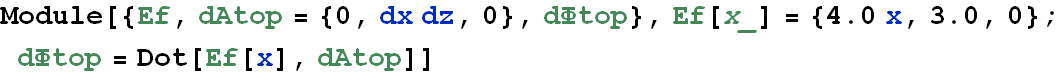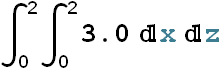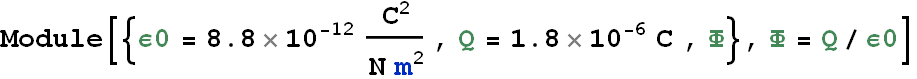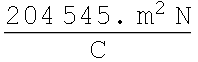Gauss’ Law
Objectives
In this chapter we will learn:
What is Flux.
How to calculate electric flux.
Gauss’s Law.
Relation between Gauss’ Law and Coulomb’s Law
How to apply Gauss’ Law to compute Electric field or charge.
What is a flux?
The word “flux” comes from the Latin word meaning “to flow”.
Rate of flow of air volume through a window (surface) is an example of a flux.
Magnitude of flux depends upon the velocity ![]() (blue arrow) of the flow with respect to area vector
(blue arrow) of the flow with respect to area vector ![]() (red arrow) of the window (surface).
(red arrow) of the window (surface).
Area is defined as a vector with its direction perpendicular to the surface (for a closed surface, the direction is always pointing outward).
The flux Φ through the window is defined as
![]()
Flux of an electric field
Flux Φ of Electric field through a plane surface of area ![]() is defined as
is defined as
![]()
If the area is of arbitrary shape, we can divide the area into small squares of area ![]() .
.
The flux Φ of electric field through such an arbitrary area can be given as
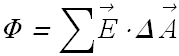
Each square should be small enough so that we can neglect the curvature.
The direction of each area vector should be normal to the surface pointing outwards.
Dot product is a scalar product so flux is a scalar quantity.
When area vector approach a definitive limit ![]() , the summation becomes integral
, the summation becomes integral
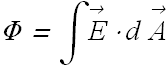
Checkpoint 1 (Flux of Electric Field)
The figure here shows a cube of face area A immersed in a uniform electric E field that has the positive direction of the z-axis.
In terms of E and A, what is the flux through
(a) the front face (which is in the xy plane),
(b) the rear face,
(c) the top face, and (d) the whole cube?
Solution
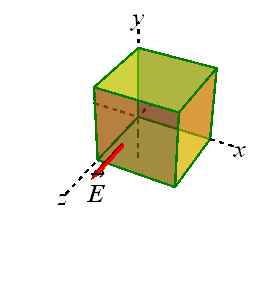
Problem 1 (Flux of Electric Field)
A nonuniform electric field given by ![]() pierces the cube of edge 2.0 m shown in the figure (E is in newtons per coulomb and x is in meters.) What is the electric flux through the right face, the left face, and the top face?
pierces the cube of edge 2.0 m shown in the figure (E is in newtons per coulomb and x is in meters.) What is the electric flux through the right face, the left face, and the top face?
Solution
Why we want Gauss’ Law?
Computing the electric field due to a distribution of charge is an involved job.
Gauss law makes those calculations extremely simple in many situations (not all situations)
Gauss’ law relates the electric field flux through a closed surface to the net charged enclosed by the surface.
A closed surface is also called a Gaussian surface. It can have any arbitrary shape.
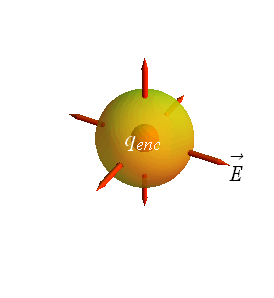
Gauss’ Law
Gauss’ law relates net flux Φ of an electric field through a closed surface (a Gaussian surface) to the net charge ![]() that is enclosed in that surface.
that is enclosed in that surface.
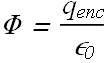
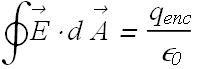
This hold only when the net charge is located in a vacuum or in air (approximately air can be treated as vacuum).
![]() is the algebraic sum of all the positive and negative charges. Therefore it can have any value, positive, negative or zero.
is the algebraic sum of all the positive and negative charges. Therefore it can have any value, positive, negative or zero.
When ![]() is positive the net flux is outward.
is positive the net flux is outward.
When the ![]() is negative the net flux is inward.
is negative the net flux is inward.
Charge outside the surface is not included in ![]() , no matter how close is that to the surface.
, no matter how close is that to the surface.
The “shape” of the surface enclosing the net charge “does not affect” the total flux as the net charge enclosed is constant
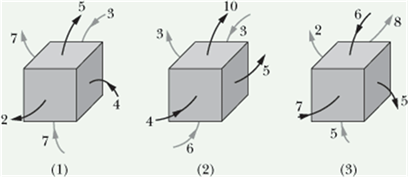
Checkpoint 2 (Gauss’ Law)
The figure shows three situations in which a Gaussian cube sits in an electric field. The arrows and the values indicate the directions of the field lines and the magnitudes (in ![]() ) of the flux through the six sides of each cube. (The lighter arrows are for the hidden faces.)
) of the flux through the six sides of each cube. (The lighter arrows are for the hidden faces.)
In which situation does the cube enclose (a) a positive net charge, (b) a negative net charge, and (c) zero net charge?
Solution
Gauss’ Law and Coulomb’s Law
For a charge q placed at the center of a spherical surface, Gauss’ law relates net flux Φ of an electric field ![]() as
as
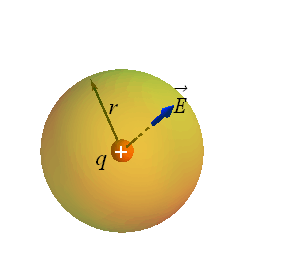
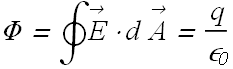
Distance of each point on the sphere surface from the center is same therefore we can assume that the magnitude of electric field ![]() on all the point on the surface is same.
on all the point on the surface is same.
Area vector ![]() is always parallel to
is always parallel to ![]() , therefore
, therefore ![]() .
.
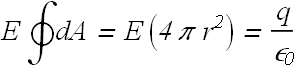
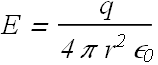
Checkpoint 3 (Gauss’ Law and Coulomb’s Law)
There is a certain net flux ![]() through a Gaussian sphere of radius r enclosing an isolated charged particle.
through a Gaussian sphere of radius r enclosing an isolated charged particle.
Suppose the enclosing Gaussian surface is changed to
(a) a larger Gaussian sphere,
(b) a Gaussian cube with edge length equal to r, and
(c) a Gaussian cube with edge length equal to 2r.
In each case, is the net flux through the new Gaussian surface greater than, less than, or equal to ![]() ?
?
Problem 2 (Gauss' Law)
A point charge of 1.8 μC is at the center of a cubical Gaussian surface 55 cm on edge. What is the net electric flux through the surface?
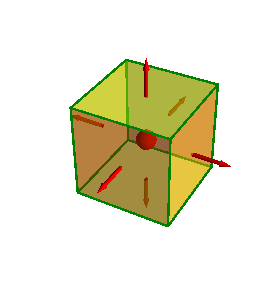
Solution
What happens when a conductor is placed inside an electric field?
Consider a conductor placed in a uniform Electric field ![]() .
.
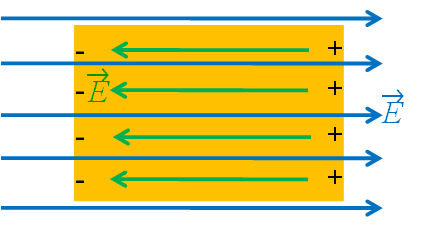
The mobile charges (electrons) in the conductor will move opposite to the field.
This redistribution of charges will produce an induced field ![]() inside the conductor.
inside the conductor.
Field ![]() will be equal in magnitude to applied field
will be equal in magnitude to applied field ![]() but opposite in direction.
but opposite in direction.
Therefore net electric field inside the conductor will be zero.
Net electric field inside a conductor is always zero.
Direction of Field due to a uniformly charged linear source
Consider a uniformly charged very long linear source.
Consider a point P at distance much smaller than the length of the linear source.
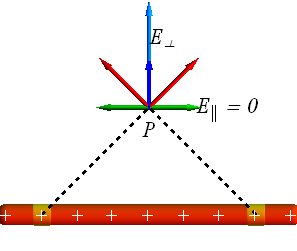
Figure clearly shows that at point P parallel components (green) of electric field due to all the contributing pieces of linear source will cancel out therefore net ![]() .
.
Net field at point P will be sum of perpendicular (blue) components ![]() of all the contributing pieces of linear source.
of all the contributing pieces of linear source.
Electric field for a uniformly charged very long linear source is always normal to the linear source.
There is no field parallel to a uniformly charged very long linear source.
Same argument is true for an infinite uniformly charged sheet.
Applying Gauss’ law: Cylindrical Symmetry
Consider a cylindrical Gaussian surface with uniformly charged linear source along its axis.
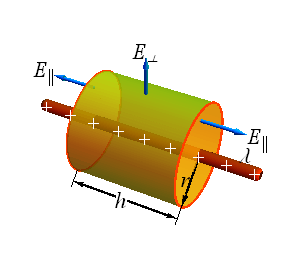
According to Gauss' Law, net flux Φ through Gaussian cylinder is related to enclosed charge ![]() .
.
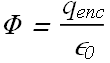
Net flux Φ of an electric field in the cylinder will be
![]()
![]()
For an infinite long source ![]() and
and ![]() , therefore
, therefore
![]()
If λ is the linear density of charge, total charge enclosed ![]() will be given as
will be given as
![]()
According to Gauss' Law
![]()
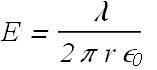
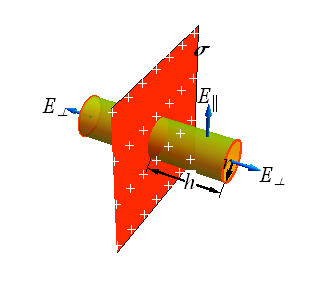
Applying Gauss’ law: Planar Symmetry
Consider a Gaussian cylinder intersecting the uniformly charged sheet.
 |
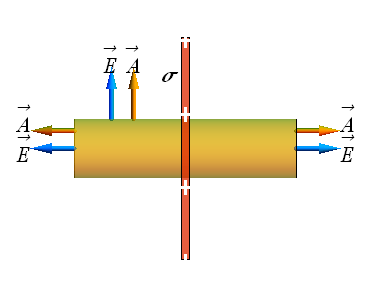 |
According to Gauss' Law, net flux Φ through Gaussian cylinder is related to enclosed charge ![]() .
.
![]()
Net flux Φ of an electric field in the cylinder will be
![]()
![]()
For an infinite long source ![]() and
and ![]() , therefore
, therefore
![]()
If σ is the surface charge density, total charge enclosed ![]() will be given as
will be given as
![]()
According to Gauss' Law
![]()
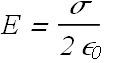
It is independent of distance from the sheet
Electric field due to a uniformly charged Spherical Shell
Consider a uniformly charged shell (cross section is shown) of radius R (red shell) with total charge Q.
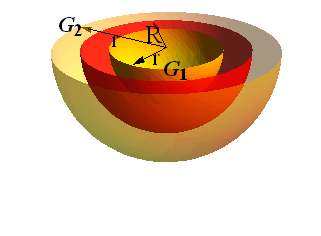
When a spherical Gaussian surface ![]() of radius r<R is inside the shell, enclosed charge
of radius r<R is inside the shell, enclosed charge ![]() , therefore
, therefore
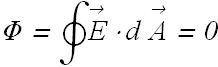
![]()
When a spherical Gaussian surface ![]() of radius r>R is out side the shell, enclosed charge
of radius r>R is out side the shell, enclosed charge ![]() .
.
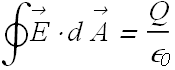
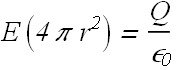
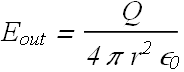
Electric field due to a uniformly charged solid sphere
Consider a uniformly charged solid sphere (red) of radius R with total charge Q.

Consider a spherical Gaussian surface of radius r>R out side the red sphere, the enclosed charge ![]() .
.
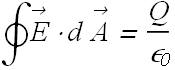
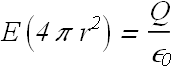
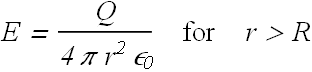
Consider a spherical Gaussian surface of radius r<R inside the red sphere, the enclosed charge ![]() is a fraction of total charge Q.
is a fraction of total charge Q.

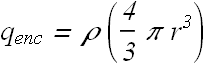
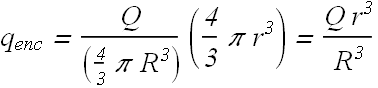
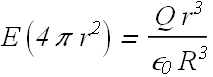
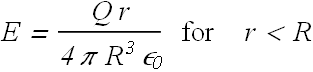
Checkpoint 4 (Gauss’ Law and Coulomb’s Law)
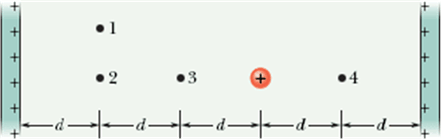
The figure shows two large, parallel, non-conducting sheets with identical (positive) uniform surface charge densities, and a sphere with a uniform (positive) volume charge density.
Rank the four numbered points according to the magnitude of the net electric field there, greatest first.
Solution:
Both the infinite sheets produce uniform electric fields equal in magnitude but an opposite in direction.
Therefore the contribution to net electric field at any point due to the sheets will be “zero”.
The field experienced at different points is only due to the positively charged sphere.
Therefore the field at 3 and 4 will equal and maximum (closer to the sphere)
point 2 will be next in magnitude and point 1 will be last (farthest from center of sphere)