Force and Motion

Objectives

Up to now we have studied “kinematics” or study of the motion of objects using parameters such as the position vector, displacement, velocity and acceleration.

We have not understood the cause of this motion.

In this chapter we will study the cause of motion or part of mechanics known as “dynamics” and following are our objectives.

Understand Newton’s laws of motion.

Study the relation between a force and the acceleration.

Understand the concept of mass.

Understand the concept of an inertial reference frame.

How to draw a free body diagram?

Understand basic structure of a solid object, this will help us in understanding source of two forces: Normal force and Tension force

Learn about gravitational force and weight.

Learn about force of friction.

Learn to solve problems involving these forces.

Limitation of Newtonian Mechanics

Newtonian mechanics is the study of relation between a force and the acceleration produced by it.

Newtonian mechanics has limitations and is not applicable in following situations.

When the speeds of the interacting bodies are very large (1% or more of the speed of light) the Newtonian mechanics has to be replaced with Einstein's special theory of relativity (1905),

Theory of relativity holds at any speed.

If the interacting bodies are on the scale of atomic structure (for example, they might be electrons in an atom), we must replace Newtonian mechanics with quantum mechanics (1926).

Newton’s First Law

A body will keep moving with constant velocity if no force acts on it.

An object moves in a straight line and at constant speed except in the absence of its interaction with other object.

Force is generated by interaction between objects.

This law only gives conceptual connection between interactions and their effect on the motion of objects.

This law does not allow us to make quantitative predictions.

We can not use this law to predict the exact trajectory of a projectile or uniform circular motion.

Let us analyze it.

Law tells us that force changes the velocity of an object.

Acceleration is change in velocity.

Therefore we can say that Force produces acceleration .

If force is zero or the object is not interacting with any object, .  

Newton’s Second Law

Experimentally it was found that acceleration of an object is proportional to the total force acting on that object.

Since acceleration is a vector quantity therefore force should also be a vector quantity.

According to Newton's second Law, the proportionality constant is known as the mass of the object.

What is mass?

Mass is an intrinsic characteristic of a body that relates a force on the body to the resulting acceleration.

Mass is a scalar quantity.

You can have a physical sensation of mass only when you attempt to accelerate a body, as in the kicking of a baseball or a bowling ball.

What happens if two or more forces act on an object?

When two or more forces act on an object we can find their "net" force , or total force, by adding individual forces as vectors.

This fact is called the "principle of superposition" for forces.

Newton's Second Law can be re written as

In unit vector notation it can be written as

Where

What kinds of forces are included in net Force?

One or more objects can be considered as a "system"

Everything not in the system is part of the "surroundings"

Net force includes only the forces that the "surroundings" (external objects) exerts on the "system" of interest.

Such forces are called external forces.

In contrast, internal forces are forces that one part of a system exerts on another part of the system.

Internal forces are not included in net force.

Checkpoint - 1

Which of the figure’s six arrangements correctly show the vector addition of forces and to yield the third vector, which is meant to represent their net force ?

Units of Force

Force produces acceleration. Thus, a force is measured by the acceleration it produces.

If we apply some force on a body of mass 1 kg kept on a frictionless surface, and this force produces 1 m/ acceleration in that body. The magnitude of that force is defined as 1 N (Newton).

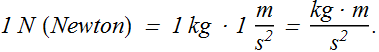
Checkpoint - 2

The figure here shows two horizontal forces acting on a block on a frictionless floor. If a third horizontal force also acts on the block, what are the magnitude and direction of when the block is (a) stationary and (b) moving to the left with a constant speed of 5 m/s?

Inertial reference frame

An inertial reference frame is one in which Newton's law of inertia is valid.

Newton's law involves measurement of force or acceleration.

In the study of relative velocity we made the following observation

When we measure acceleration of an object from two reference frames and the frames are moving with constant velocities. The measured values of acceleration in both the frames, turns out to be same.

This means all the reference frames moving with constant velocity are inertial reference frames.

In other words any non-accelerating object is an inertial reference frame.

All accelerating reference frames are non-inertial.  

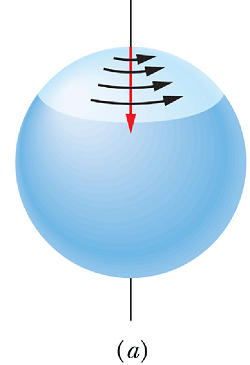
Is our earth an inertial reference frame?

We know that earth is rotating around its axis and around sun

A rotating object is an accelerating object; therefore earth is a non inertial reference frame.

Suppose we observe a puck sliding with constant velocity from North pole towards South pole on a long ice strip.

Standing on the earth, its path will observe like the red line shown in Fig. b.

Observed deflection is without any force so, this is violation of Newton's Law and proves that Earth is a non inertial reference frame.

For many practical situations we assume earth to be an inertial reference frame.

Suppose the puck is sent sliding along a short strip.

In this situation the deflection will be negligible and earth can be assumed to be an inertial reference frame.

Free Body Diagram

Part of the procedure of solving a mechanics problem using Newton’s laws is drawing a free body diagram.

First we choose the object to be studies and we call it a “system” of objects (It could be one object or more object).

Draw the system as a point.

Now choose the axes and draw all the external forces acting on the system.

Internal forces are not included. Let us look for horizontal external forces in following examples.

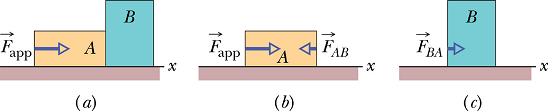
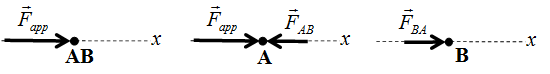
Fig. (a) System = Block A + Block B. External Force is only .

Fig. (b) System = Block A. There are two external forces and .

Fig. (c) System = Block B. There is one external force .   

Problem - 1

Two horizontal forces act on a 1.8 kg chopping block that can slide over a frictionless kitchen counter, which lies in a xy plane. One force is . Find the acceleration of the chopping block in unit - vector notation for each of the following second forces. (a) (b) (c)

The Gravitational Force

Any two objects attract each other with force called gravitational force.

Here when we speak of the gravitational force on a body, we usually mean a gravitational force that pulls on it directly toward the center of Earth.

Here we assume that the ground is an inertial frame.

If we neglect the effect of air, the only force acting on the body is the gravitational force .

Suppose a body of mass m is in free fall with the free fall acceleration g.

According to Newton’s second law :

Can you answer?

You are given a copper block and you know that it is made up of several copper atoms.

Why not these atoms spontaneously evaporate or fall apart?

Why is it very difficult to compress the block and reduce its size?

Atoms and ball - spring model

All matter consists of atoms, whose typical radius is about meter.

Atoms in all the materials attract each other when they are close to each other but not too close, that is why the metal does not spontaneously evaporate or fall apart from the block.

Atoms repel each other when they get too close to each other, that is why it is very difficult to compress the block, so the atom must resist an attempt to push them closer

Evidently atoms in the block are just at right distance from each other, neither too close nor too far away.

This just right distance is called "equilibrium" distance between atoms.

Atoms and ball - spring model

Consider two balls connected with a spring.

If we try to take these balls apart (Click hold and drag any one ball), the spring will try to bring them close. So we can say balls attract each other when we try to take them apart.

If we try to bring balls closer (click hold and drag any one ball), the compressed spring try to move them apart. So we can say balls repel each other when they get too close to each other.

If you release the balls (click play) the balls will come back to their equilibrium positions (dotted lines).

This means balls do not experience any force (or balls are in equilibrium) when spring is neither stretched nor compressed.

A ball - spring model for a solid object

Since a ball spring model behaves like a two atom system. Therefore we can create a simple model of a solid object by joining several ball spring systems. As  solid object contains many atoms not just two.

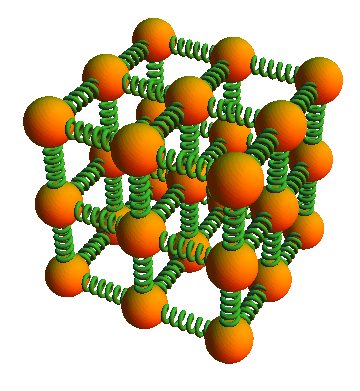
The lattice shown in the figure is the simplest kind of crystal but it has all the features we need to understand a rigid body.

This model indicates that, all “rigid” bodies are to some extent elastic, which means they will exert force if we try to change their dimensions slightly by pulling, pushing, twisting, or compressing them.

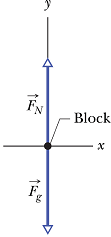
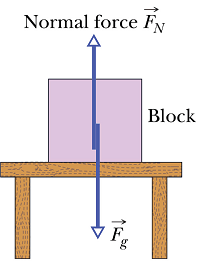
The Normal Force

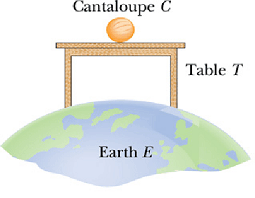
When a block of mass m is kept on a table or floor, the gravitational force pulls it down, but the block remains stationary.

This means the net force acting on the block is zero.

From where the balancing force is coming?

Analysis of Normal force

Two forces and are acting on the block, therefore net force on the block is.

Free body diagram of the block is shown in the figure.

Now suppose the table and block are moving vertically with an acceleration .

According to Newton's second law

By substituting the value of and moving it to RHS we get magnitude of normal force

Weight

The weight W of a body is the magnitude of the force required to prevent the body from falling freely on the ground.

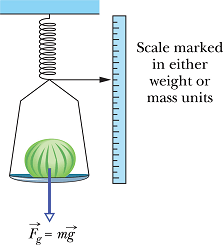How many forces are acting on the object (cantaloupe)?

Two forces are acting on the body: a downward gravitational force and a balancing upward normal force of magnitude W.

Consider a body that has vertical acceleration relative to the ground, which we again assume to be an inertial frame.

We can write Newton's second law for a vertical y axis, with the positive direction upward, as

Therefore magnitude of normal force is preventing the object from falling.

Therefore magnitude W of normal force is called the weight of the object (cantaloupe) and is given as

When vertical acceleration of an object is zero, the weight W of the object is equal to the magnitude Fg of the gravitational force on the body.

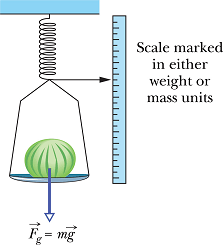
Apparent weight

What if the vertical acceleration relative to the ground?

This can be true if scale is hanging in an accelerating elevator.

If the cantaloupe and scale are accelerating vertically say in an elevator with acceleration, according to Newton's law

Therefore weight W (magnitude of ) is

is positive if elevator is accelerating upward.

is negative if accelerating downwards.

Apparent weight of an object is always equal to the normal force acting on the object.

If the cantaloupe and scale are not accelerating vertically , the apparent weight of the block will be equal to its real weight.

Checkpoint - 3

Is the magnitude of the normal force  greater than, less than, or equal to mg if the block and table are in an elevator moving upward (a) at constant speed and (b) at increasing speed?

Tension Force

When a block of mass m is hanging on a cord (or a rope, cable, or other such object), the gravitational force pulls it down, but the block remains stationary.

This means the net force acting on the block is zero.

From where the balancing force is coming?

Characteristics of Tension Force :

Tension has the following characteristics:

It is always directed along the rope

It is always pulling the object

It has the same value along the rope.(for example between points A and B)

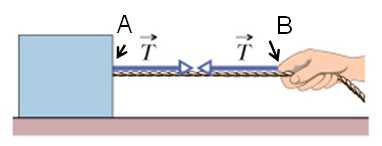
A cord is often assumed to be mass less (meaning its mass is negligible compared to the body's mass) and un-stretchable.

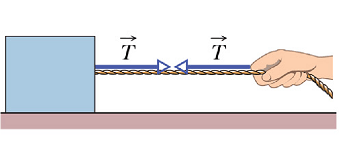
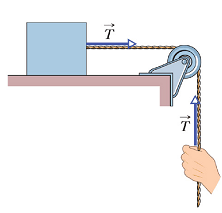
Some points to be remembered about tension force

Even if the cord runs around a pulley, It pulls on both bodies with the same force magnitude of .

The direction of the tension force pulling the object, always remains along the cord, even if it has gone around the pulley.

Force of tension remains even if the bodies are accelerating.

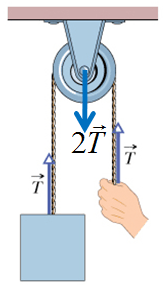
If the cord wraps halfway around a pulley, the net force on the pulley from the cord has the magnitude 2T.

Checkpoint - 4

The suspended body in the figure, weighs 75 N. Is T equal to, greater than, or less than 75 N when the body is moving upward (a) at constant speed, (b) at increasing speed, and (c) at decreasing speed?

Recipe for the application of Newton' s law of motion.

Choose the system to be studied.

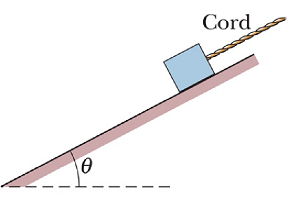
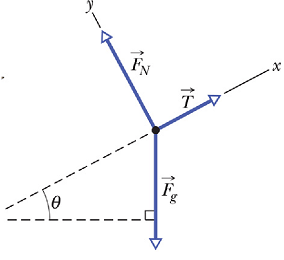
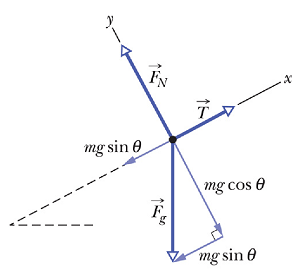
Make a simple sketch of the system, Fig. (a)

Identify all the forces that act on the system. Label them on the diagram.  

Draw the free body diagram with all the external forces acting on the system to be studied, Fig. (b)

Choose a convenient coordinate system.

Compute components of the forces not parallel to any axis, Fig. (c).

Calculate components of the net force.

Apply Newton’s  second law of motion to the system.

(a)	(b)	(c)

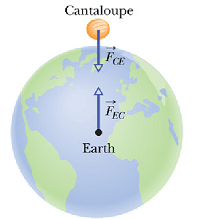
Newton’s Third Law

Consider a book and a crate in the figure.

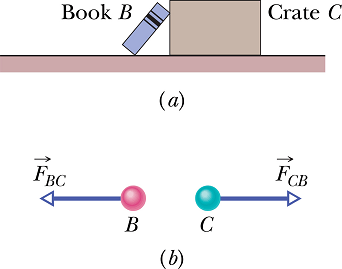
If the book exert a force on the crate, then according to Newton's third law the crate will exert a force on the book such that

Where minus sign means two forces are in opposite direction. We can call the forces between two bodies a third-law force pair.

Newton’s Third Law: When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction.

Checkpoint 5

Suppose that the cantaloupe and table in the figure are in an elevator cab that begins to accelerate upward. (a) Do the magnitudes of   and increase, decrease, or stay the same? (b) Are those two forces still equal in magnitude and opposite in direction? (c) Do the magnitudes of and increase, decrease, or stay the same? (d) Are those two forces still equal in magnitude and opposite in direction?

Uniform Circular Motion

We know that when a body moves in a circle (or a circular arc) of radius R at constant speed v, it is said to be in uniform circular motion.

The body has a centripetal acceleration of constant magnitude given by

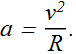
What is the direction of ?

If we look at the following simulation, is always directed toward the center of the circle.

Any object moving along a circle, always has centripetal acceleration directed towards its center.

Checkpoint 6

When you ride in a Ferris wheel at constant speed, what are the directions of your acceleration and the normal force on you (from the always upright seat) as you pass through
(a) the highest point and
(b) the lowest point of the ride?

Problem - 2

In the figure, a car is driven at constant speed over a circular hill and then into a circular valley with the same radius. At the top of the hill, the normal force on the driver from the car seat is 0. The driver’s mass is 70.0 kg.

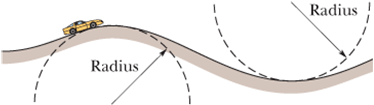
What is the magnitude of the normal force on the driver from the seat when the car passes through the bottom of the valley?

Solution :

At the top of the Hill, net force is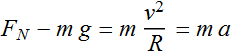

At the bottom of the Hill, net force is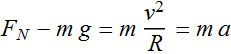

Friction Force

When we slide or try to slide an object over a surface, the motion is resisted by a bonding between the object and the surface.

The resistance is called frictional force or simply friction

Static frictional force

When we exert force in an attempt to pull a block to the left, a frictional force is directed to the right.

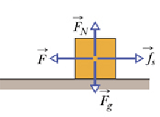
This force exactly cancels our force and the block does not move.

This frictional force is called the static frictional force .

Now as we increase the magnitude of the applied force, the magnitude of the static frictional force also increases and the block remains at rest.

Kinetic frictional force

But when the applied force reaches a certain magnitude, however, the block “breaks away” from its intimate contact with the surface and accelerates leftward.

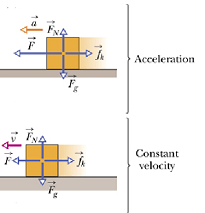
The friction force is still present, and opposes the motion.

This frictional force which opposes the motion is called the kinetic frictional force.

Magnitude of Friction force

When we apply a force to the block and it does not move, what will be its acceleration?

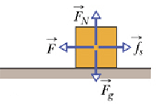
But when the magnitude of applied force reaches a certain maximum value, the block “breaks away” and start moving.

This is the maximum static force of friction the block can produce.

Experimentally magnitude of maximum static force of friction is found to be proportional to the magnitude of normal force

where is the coefficient of static friction and   is the magnitude of the normal force on the body from the surface.

When the magnitude of the applied force exceeds , the body begins to slide along the surface.

When the body begins to slide along the surface or body is in motion, the magnitude of the frictional force rapidly decreases and is called the kinetic frictional force .

Experimentally magnitude of kinetic frictional force is found to be proportional to the magnitude of normal force .

where is the coefficient of kinetic friction.

Magnitude of kinetic frictional force   is always less than the magnitude of maximum static force of friction .

Checkpoint 7

A block lies on a floor.
(a) What is the magnitude of the frictional force on it from the floor?
(b) If a horizontal force of 5 N is now applied to the block, but the block does not move, what is the magnitude of the frictional force on it?
(c) If the maximum value  of the static frictional force on the block is 10 N, will the block move if the magnitude of the horizontally applied force is 8 N?
(d) If it is 12 N?
(e) What is the magnitude of the frictional force in part (c)?  

Problem - 3

In the figure, blocks A and B have weights of 44 N and 22 N, respectively.  

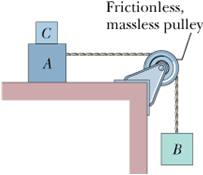
Determine the minimum weight of block C to keep A from sliding if between A and the table is 0.20.

Block C suddenly is lifted off A. What is the acceleration of block A if between A and the table is 0.15?

Solution :

When Block B is not sliding, its acceleration is zero. Consider forces on Block B when it is not sliding:

When Block A and C are not sliding, their acceleration is zero. Consider horizontal forces on Block A & C when it is not sliding:

When Block C is suddenly taken off, Block A will slide with acceleration a. Now net horizontal forces on Block A will be equal to  its mass times acceleration:

Problem - 4

A puck of mass m=1.50kg slides in a circle of radius r=20.0cm on a frictionless table while attached to a hanging cylinder of mass m=2.50kg by a cord through a hole in the table (See Figure).   

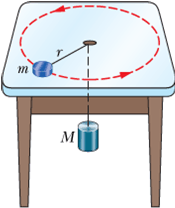
What speed keeps the cylinder at rest?

Solution :

Suppose the puck is rotating with constant speed v in a circle of radius r=20.0cm.

The tension force T will always act perpendicular to the direction of the velocity of puck.

Net force on the puck

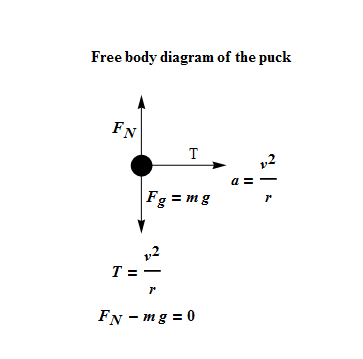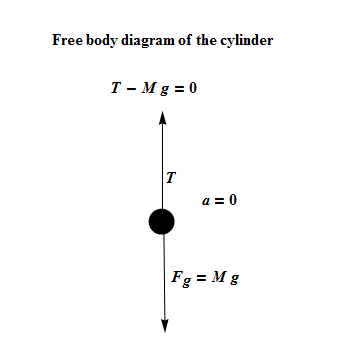When we consider only the Hanging Cylinder as a system, the net force is in a circle of radius r=20.0cm

Problem - 5

In the following figure, a 1.34 kg ball is connected by means of two mass-less strings, each of length L=1.70m, to a vertical, to a rotating rod. The strings are tied to the rod with separation d=1.70m and are taut. The tension in the upper string is 35 N.    

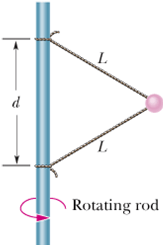
What is the tension in the lower string?

What is the magnitude of the net force on the ball?

What is the speed of the ball?

What is the direction of ?