Electromagnetic Waves
Objectives
The connection between electric and magnetic fields to produce light is one of the greatest achievements produced by physics.
Electromagnetic waves are at the core of many fields in science and engineering.
In this chapter we will learn about:
Maxwell's law of induction.
How electromagnetic waves are generated?
Why light waves were predicted to be electromagnetic waves.
Optics
Laws of reflection.
What is chromatic dispersion?
Total internal reflection.
Maxwell's law of induction
According to Faraday's law, a changing magnetic flux induces an electric field
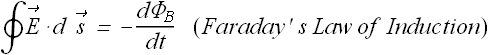
Maxwell using an elegant symmetry arguments predicted that a changing electric field should induce a magnetic field.
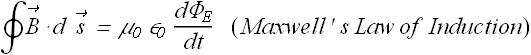
Although Maxwell predicted the existence of induced magnetic field by changing electric field but the results were experimentally verified later.
How can we show that Maxwell' s prediction is correct?
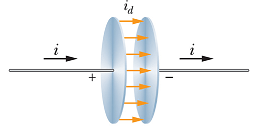 |
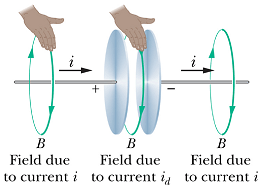 |
Consider a charging capacitor. If charge q on the plates is changing, the current through the wires is
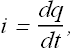
Consider a loop of radius r around the wire, as per Ampere's law
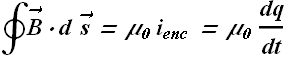
Or
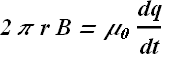
Move the loop closer and closer to the plates, we will get same value of B until the loop enters the space between the plates.
There is no current flowing between the plates (enclosed current is zero), therefore as per Ampere's law, the magnetic field should disappear.
That will be quite strange.
Let us apply Maxwell's law of induction in the space between the plates.
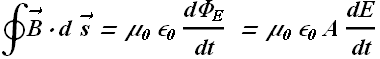
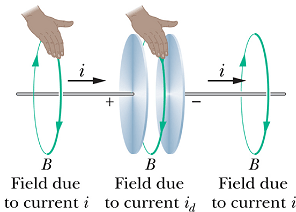
When q is the charge on the capacitor plates, as per Gauss's law electric field E between the plates is
![]()
Where A is the area of the plates.
Combine the above two equations.
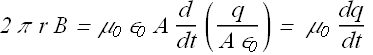
We get the same value of B as we obtained with Ampere's law around the wire.
This means by moving the loop along the whole circuit will not change the magnitude of B.
Ampere's law is incomplete?
We have observed that Ampere's law alone, does not explain the magnetic field around the plates of the charging capacitor.
Complete law of induction should be
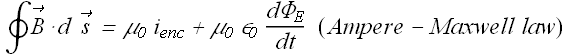
This is called Ampere-Maxwell's law of induction.
The term ![]() on right hand side has the dimensions of current and is also called displacement current
on right hand side has the dimensions of current and is also called displacement current ![]() .
.
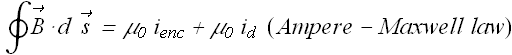
Displacement current is a fictitious current.
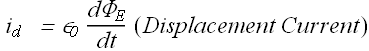
Checkpoint 1
The figure shows graphs of the electric field magnitude E versus time t for four uniform electric fields, all contained within identical circular regions of a capacitor. Rank the fields according to the magnitudes of the magnetic fields they induce at the edge of the region, greatest first.
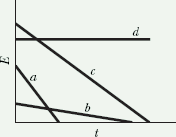
Hint : On an t vs. E graph, the slope is equal to dE/dt. Magnitude of induced magnetic field is proportional to the change in electric field.
How electromagnetic waves are generated?
Let us consider a neutral sheet of charges in yz-plane with equal number of positive and negative charges.
The sheet is electrically neutral so there is no static electric field due to the sheet.
Let us give instantaneously a velocity u to the negative charges in the -y direction. So we suddenly have a surface current J in the y-direction (J is the current per unit length along z axis).
What will happen when the current change from zero to some finite value?
According to Ampere’s law a magnetic field will be generated in the minus z-direction for x > 0 and in the opposite direction for x < 0.
Now what will happen when the magnetic field change from zero to a finite value?
According to Faraday's law of induction it will generate electric field E.
These induced magnetic and electric fields will not reach at each point of space, instantaneously. They will have some finite velocity say v.
These fields will make their way forward like a tidal wave, with a front moving at a uniform velocity v.
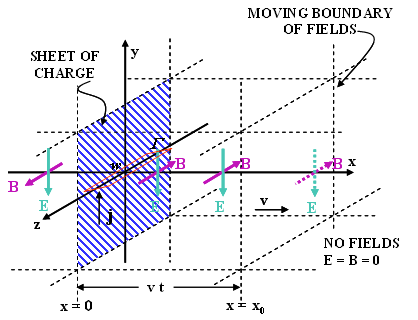
The magnitude of B can be computed by drawing a close loop Γ of width w around the sheet.
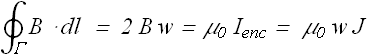
Let us view the field from one side and draw a loop ![]() with half of its part in the space where the fields are uniform and half of its part in where the fields have not reached yet.
with half of its part in the space where the fields are uniform and half of its part in where the fields have not reached yet.
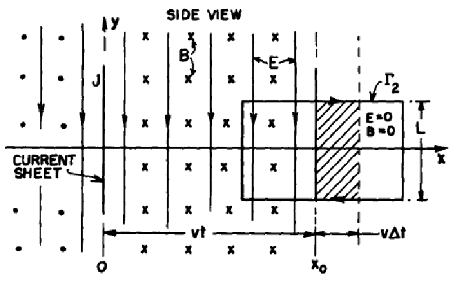
As the magnetic field is moving with speed v, Electric field will be induced and according to Faraday's Law
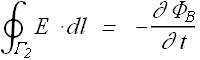
Change in magnetic flux through loop ![]() is
is
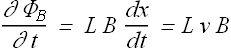
Similarly the line integral on loop ![]() gets contribution only from the side which is inside the field as on the outside segment, field has not yet reached. Contribution of top and bottom sides get canceled out.
gets contribution only from the side which is inside the field as on the outside segment, field has not yet reached. Contribution of top and bottom sides get canceled out.
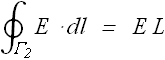
Substituting the value of line integral and rate of change of flux in the Faraday's equation we get
![]()
Now let us view the figure from the top and draw a loop ![]() again with half of its part in the space where the fields are uniform and half of its part in where the fields have not reached yet.
again with half of its part in the space where the fields are uniform and half of its part in where the fields have not reached yet.
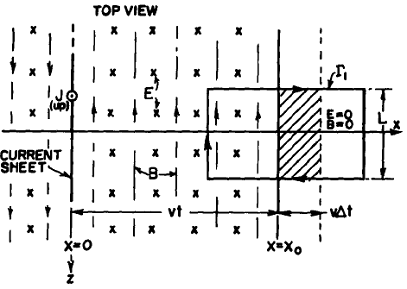
Now according to Maxwell's law of induction the magnetic field should be related to changing Electric field
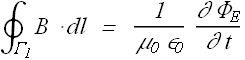
Change in Electric field flux through loop ![]() is
is
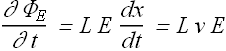
Similarly the line integral of magnetic field on loop ![]() gets contribution only from the side which is inside the field as on the outside segment, field has not yet reached. Contribution of top and bottom sides get canceled out.
gets contribution only from the side which is inside the field as on the outside segment, field has not yet reached. Contribution of top and bottom sides get canceled out.
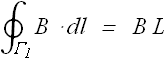
Substituting the value of line integral and rate of change of flux in the Maxwell's equation of induction we get
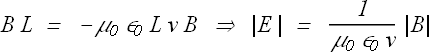
From Faraday's law of induction we get
![]()
From Maxwell's law of induction we get
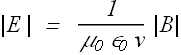
These two equations can only be true if
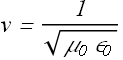
It turn out that ![]() is the speed of light.
is the speed of light.
This shows that when ever there is a change in electric current, it induces both electric and magnetic fields which propagate with the speed of light in free space.
We can say that electromagnetic influence (electromagnetic fields) propagates with speed of light in free space.
Now what happens if we suddenly put off the current after a short interval of time T.
We can use the law of superposition to compute the net fields.
Let us assume that suddenly after a short interval T of starting the motion of negative charges along negative y direction, the positive charges also start moving in negative y direction.
This generates an exactly equal current in opposite direction.
This will also induce the moving (with speed v=c) electric and magnetic fields of same magnitude as before but now in opposite direction (Figure b).

At any position along the x axis if the fields generated by first current reaches at time t, the field generated by the opposite current will reach at time (t - T) as shown in figure (b).
Now according to law of superposition the net field will be as shown in figure (c).
The fields are zero for x>c t, they are constant between x=c (t-T) and x=c t, and again zero for x<c (t-T).
In short a current pulse of duration T in the sheet, generates a short pulse of electromagnetic fields which leave the current sheet and travel through the space on its own (no longer connected to the source) with a velocity equal to speed of light.
This led Maxwell to conclude that light is a traveling wave of electric and magnetic fields—an electromagnetic wave—and thus that optics, the study of visible light, is a branch of electromagnetism.
Maxwell’s Rainbow
In Maxwell's time (the mid 1800s), the only electromagnetic waves known were visible, infrared, and ultraviolet forms of light.
Later Heinrich Hertz discovered what radio waves also move with same speed as visible light.
We know now a wide spectrum of electromagnetic waves: Maxwell's Rainbow.
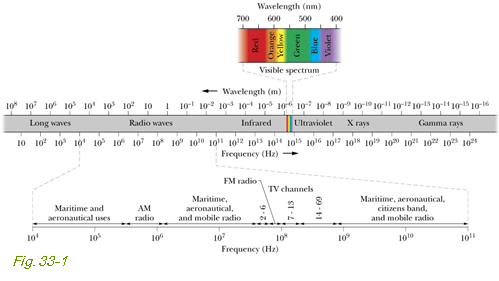
Visible is only a tiny fraction of the entire electromagnetic spectrum.
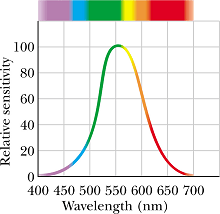
Green color is at the peak of Visible spectrum, or we can say human eye response is maximum for green color.
How can we generate Traveling Electromagnetic (EM) Wave?
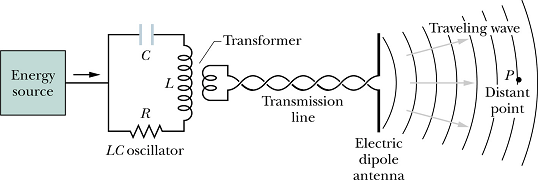
An LC circuit can produce oscillating charges or sinusoidally oscillating currents.
If we couple this oscillating current to an antenna (called electric dipole antenna) with the help of a transformer, the charges in the antenna will also start oscillating with same frequency.
The oscillating charges will in turn produce oscillating electric and magnetic fields, which then propagate through space as ElectroMagnetic (EM) waves.
Oscillating angular frequency ω of this source will be
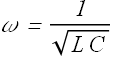
Mathematical Description of Traveling EM Waves
A sinusoidally oscillating charge with angular frequency ω, will induce sinusoidally oscillating and traveling magnetic field wave B.
![]()
Oscillating and traveling magnetic Magnetic field wave B will induce electric field wave E.
![]()
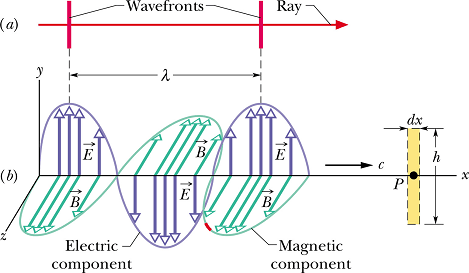
![]()
We know that speed of a wave is given as
![]()
λ is known as the wavelength of the wave.
For an electromagnetic wave, the ratio of electric and magnetic field magnitudes is
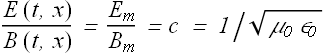
A Most Curious Wave
Unlike all other waves, EM waves require no medium to travel.
EM waves can travel through empty space (vacuum)!
Speed of light is independent of speed of observer!
You could be heading toward a light beam at the speed of light, but you would still measure c as the speed of the beam!
![]()
Reflection and Refraction
Although light waves spread as they move from a source, often we can approximate its travel as being a straight line.
Study of light is called Optics.
In most of circumstances, light can be treated as a ray traveling in straight line.
When we make such assumptions about light to study its properties, we call this branch of optics, geometrical optics.
What happens when a narrow beam of light encounters a glass surface?

You can see it bends from its path in the glass.
It generates another light beam which is bouncing back but at another angel.
Bending of light is called Refraction.
Generation of another beam is called Reflection.
Why reflection and refraction takes place when a narrow beam of light encounters a glass surface?
The speed of light in glass is less than its speed in air or vacuum.
This difference in speed cause this phenomenon of reflection and refraction.
The ratio of speed v of light in a medium to its speed c in vacuum is called refractive index n.
![]()
Laws of Reflection and Refraction :
Consider a light beam entering from one medium of refractive index ![]() (say air) to another medium of refractive index
(say air) to another medium of refractive index ![]() (say glass).
(say glass).
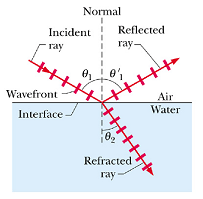
The orientation angle of the beam is measured with respect to a line normal to the interface surface of two mediums.
![]() is called angle of incidence.
is called angle of incidence.
![]() is called angle of reflection and
is called angle of reflection and ![]() is called angle of refraction.
is called angle of refraction.
Experiments have shown that the reflection and refraction are governed by two laws.
Law of reflection:
![]()
Law of refraction:
![]()
This is called Snell's law of refraction.
Reflections in different kind of materials :
For light going from n1 to n2:
If ![]() then
then ![]()
If ![]() then
then ![]() , light bent toward normal
, light bent toward normal
If ![]() then
then ![]() , light bent away from normal
, light bent away from normal
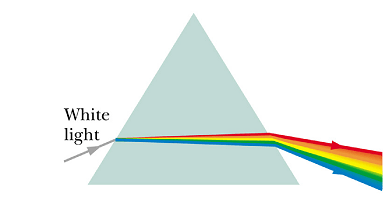
Chromatic Dispersion
Refractive index n (index of refraction) of any medium except vacuum depends on the wavelength of the light.
So if light consisting of different wavelengths enters a material, the different wavelengths will be refracted differently.
This phenomenon is called chromatic dispersion.
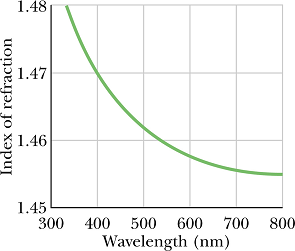 |
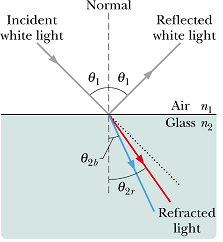 |
Chromatic dispersion can be good (e.g., used to analyze wavelength composition of light) or bad (e.g., chromatic aberration in lenses).
Example of Good Chromatic Dispersion
It can be used to analyze wavelength composition of light.
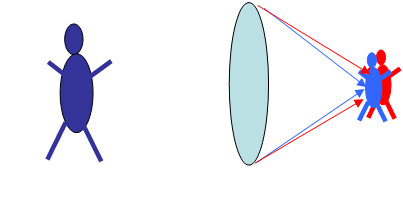
Example of Bad Chromatic Dispersion
Chromatic aberration in lenses can distort or blur the image in a Camera.
Total Internal Reflection :
Change angle of incidence ![]() in following simulation.
in following simulation.
As long as ![]() , we can see that
, we can see that ![]() .
.
What happens when ![]() , keep increasing the incidence angle
, keep increasing the incidence angle ![]() ?
?
What we saw that at a certain value of ![]() , the refracted beam (also known as transmitted beam) disappears and only reflected beam is there.
, the refracted beam (also known as transmitted beam) disappears and only reflected beam is there.
This phenomenon is called total internal reflection, the incidence beam gets totally reflected at the interface.
Critical Angle
The incidence angle ![]() at which total internal reflection takes place is called critical angle
at which total internal reflection takes place is called critical angle ![]() .
.
You can see in the simulation, when angle of incidence ![]() is equal to critical angle, angle of refraction
is equal to critical angle, angle of refraction ![]() .
.
![]()
From the above equation we can get the value of critical angle in terms of refractive index ![]() , and
, and ![]() .
.
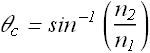
For incidence angle ![]() , Snell's law is not applicable.
, Snell's law is not applicable.
Example of total internal reflection :
Transportation of light using a fiber-optic cable is the best example of total internal reflection. Light does not leaks out of the optical fiber due to total internal reflection on its side walls.
Rainbows
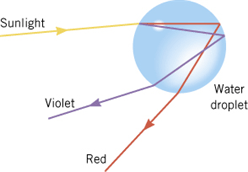
Primary Rainbow
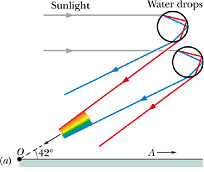
Sun light enters from air to a water droplets and gets refracted.
The refracted rays are reflected twice off the back surface.
 |
 |
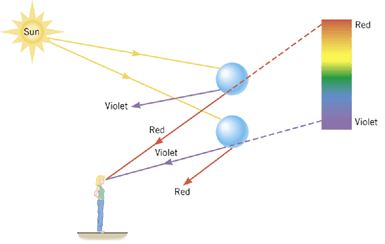 |
The range of angles for the exiting ray will depend on the color of the ray (water refractive index is different for different wavelengths).
Blue is refracted more strongly than red, only droplets that are closer to the rainbow center (A) will refract/reflect blue light to the observer (O).
Droplets at larger angles will still refract/reflect red light to the observer.
Formation of this rainbows involves one reflection of light inside each drop, they are often called primary rainbows.
This rainbow is always a 42° circular arc around observation point A.
Top of a rainbow is never more than 42° above the horizon.
Secondary Rainbow
What happens for rays that reflect twice off the back surfaces of the droplets?
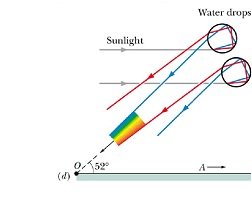
It will generate, what is called secondary rainbow.
A secondary rainbow involves two reflections inside a drop.
Colors appear in the secondary rainbow at an angle of 52° from the direction of A.
A secondary rainbow is wider and dimmer than a primary rainbow and thus is more difficult to see.
Also, the order of colors in a secondary rainbow is reversed from the order in a primary rainbow.
