Electric Field
Objectives
In this chapters we will learn
concept of “electric field”
To calculate field generated by a point charge.
Application of principle of superposition to determine the electric field created by a collection of point charges as well as continuous charge distributions.
Calculate electric force from electric field
Notion of “electric dipole.”
To determine net force and net torque, exerted on an electric dipole by a uniform electric field.
What is a Field?
Assignment of a quantity or number to each point in space is called the field of that quantity.
What is Electric Field?
Consider a ball hanging with a thread.
Put some positive charge on it (Click the PLAY button to charge the ball), What we observe?
The ball gets pulled or pushed towards right by some invisible force.
Now increase the charge by "Change charge" slider. What happens now?
What can we conclude?
It seems that there is "something invisible" at the location of ball, waiting to interact with the charge of a particle .
This "something invisible" is called the "Electric Field."
We know that this "something invisible" is produced by other charges in space, therefore we can state:
"Electric Field" is a kind of invisible influence of a charge or charges at different locations in space, which can be experienced by other charge or charges.
Definition of Electric Field
"Electric field" is invisible but we can still measure it.
Let us release a known positive test charge ![]() of mass m at a point P.
of mass m at a point P.
It moves, therefore we can measure its acceleration ![]() .
.
From acceleration ![]() , we can compute the force
, we can compute the force ![]() experienced by test charge
experienced by test charge ![]() due to invisible "electric field" due to other surrounding charged objects.
due to invisible "electric field" due to other surrounding charged objects.
![]()
Now the Electric field vector ![]() at releasing point P is defined as
at releasing point P is defined as
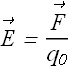
SI units of electric field are N/C (Newton/Coulomb)
Test charge can be positive or negative.
By convention, the direction of ![]() points in the direction of measured force
points in the direction of measured force ![]() experienced by a positive test charge
experienced by a positive test charge ![]() .
.
Direction of ![]() will points opposite to measured
will points opposite to measured ![]() if test charge
if test charge ![]() is negative.
is negative.
Checkpoint 1 (Electric Field)
At an observation point we found that direction of electric field ![]() points to North.
points to North.
(a) What will be the direction of force ![]() experienced by a positive charge at that point.
experienced by a positive charge at that point.
(b) What will be the direction of force ![]() experienced by a negative charge at that point.
experienced by a negative charge at that point.
Electric field of a point charge
To compute electric field at point P due to a charge Q, first we need to calculate force ![]() on a test charge
on a test charge ![]() .
.
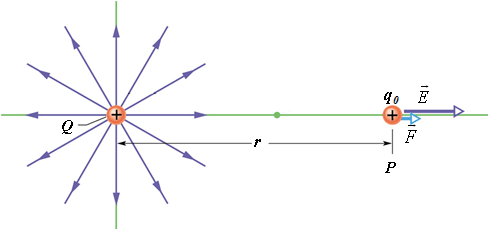
As per Coulombs law, force ![]() on
on ![]() due to Q at point P is given as
due to Q at point P is given as
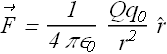
Now electric field is defined as
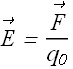
Therefore electric field of a point charge Q at point P is
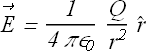
If Q is a positive charge, direction of electric field ![]() is away from the charge Q.
is away from the charge Q.
If Q is a negative charge, direction of electric field ![]() is towards the charge Q.
is towards the charge Q.
Electric Field Lines
Electric field can be represented by drawing field lines.
 |
 |
Electric field lines represent the path of a positive test charge (generally test charge amount is very small).
Electric field lines extend away from positive charge (where they originate) and towards negative charge (where they terminate).
These days we no longer attach much reality to these lines.
But these electric field of lines still provide a nice visualization of electric field.
Principle of superposition for the electric field
To measure electric field at any point due to many charges, we need to calculate net electrostatic force on a test charge ![]() .
.
Electrostatic force on any charge ![]() due to other charges in the surroundings follows the principle of superposition. (Alt click and create more surrounding charges)
due to other charges in the surroundings follows the principle of superposition. (Alt click and create more surrounding charges)
Net electrostatic force ![]() on a point test charge
on a point test charge ![]() due to other charges in the surrounding is given as
due to other charges in the surrounding is given as
![]()
Electric field ![]() at the position of test charge
at the position of test charge ![]() due to
due to ![]() ,
, ![]() ,
, ![]() , etc. is defined as
, etc. is defined as

It shows that electric field, at the location of test charge ![]() , is again obtained by superposition of electric field due to surrounding charges
, is again obtained by superposition of electric field due to surrounding charges ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
![]()
If there are N number of charges, electric field at any point P will be vector sum of fields at that point due to all the charges.
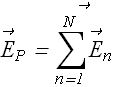
Checkpoint 2 (Electric Field due to a point charge)
The figure here shows a proton p and an electron e on an x axis.
What is the direction of the electric field due to the electron at
(a) point S?
(b) point R?
What is the direction of the net electric field at
(c) point R?
(d) point S?
![]()
Electric Dipole
A system of two equal charges of opposite sign (±q) separated by distance s apart is known as an "electric dipole."
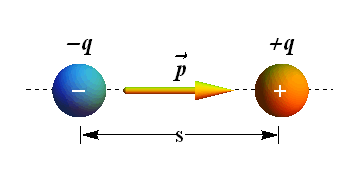
For every electric dipole we associate a vector ![]() known as the electric “dipole moment"
known as the electric “dipole moment"
![]() is defined as
is defined as
![]()
The direction of ![]() is along the line that connects the two charges and points from – q to +q.
is along the line that connects the two charges and points from – q to +q.
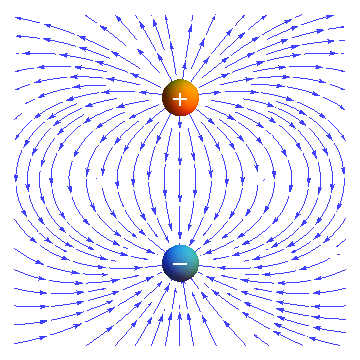
Electric Field of a dipole :
Field lines start from the positive charge and ends at the negative charge.
Naturally occurring Electric Dipoles
Many molecules have a built-in electric dipole moment. Water molecule ![]() and HCl are two such examples.
and HCl are two such examples.
Water Molecule ![]()
![]() involves ten shared electrons (8 from Oxygen and 2 from two Hydrogen atoms).
involves ten shared electrons (8 from Oxygen and 2 from two Hydrogen atoms).
Eight protons in Oxygen atom try to attract these electrons more towards Oxygen atom.
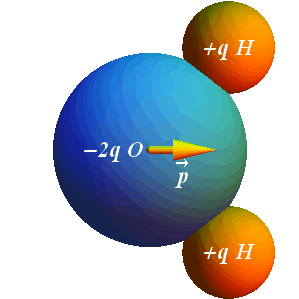
This shifting of 10 electrons more towards Oxygen, makes the Oxygen atom little negative and the two H atoms little positive.
HCl Molecule
HCl involves eighteen shared electrons (17 from Chlorine and 1 from Hydrogen atom).
Seventeen protons in Chlorine atom try to attract one Hydrogen electron more towards Chlorine atom.
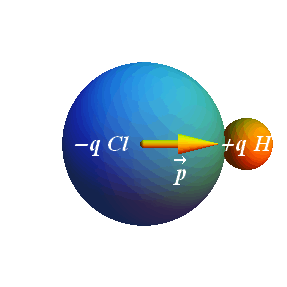
This shifting of 18 electrons more towards Chlorine, makes the Cl atom little negative and the H atom little positive.
Yellow arrow is the dipole moment vector ![]() .
.
Electric Field of an Electric Dipole
Consider a dipole with equal and opposite charges (±q) separated by distance s.
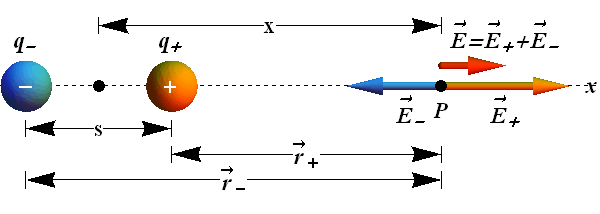
Net electric field ![]() at point P along z-axis should be sum of electric fields due to the two charges at that point.
at point P along z-axis should be sum of electric fields due to the two charges at that point.
![]()
Let us compute ![]() due to positive charge
due to positive charge ![]() .
.
![]()
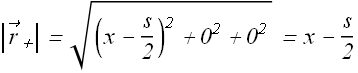
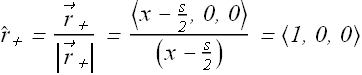
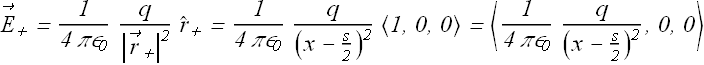
Similarly electric field ![]() due to negative charge
due to negative charge ![]() can be computed.
can be computed.
![]()
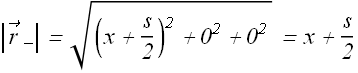
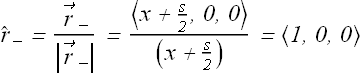
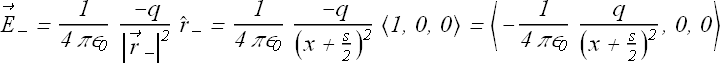
Net electric field ![]() at P can be computed as
at P can be computed as
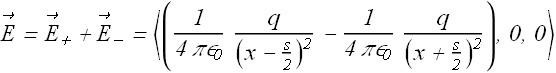
Magnitude of electric field ![]() at P is
at P is
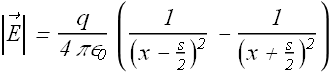
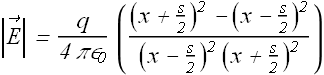
After simple algebra we get
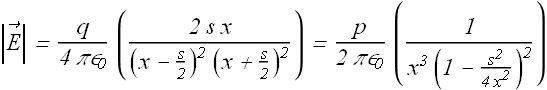
If s<<x, we can neglect ![]() in comparison to x, therefore the field at distance much larger than separation of dipole we get
in comparison to x, therefore the field at distance much larger than separation of dipole we get
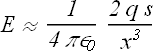
In terms of dipole moment p=q s, we can write
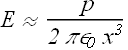
Electric field due to a Continuous Charge Distribution
Divide the charge distribution into small elements.

Treat each element as a point charge.
Calculate electric field ![]() due to each element at point P.
due to each element at point P.
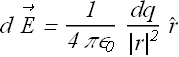
Vectorially add the fields due to all the elements.
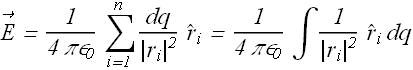
If the charge distribution is uniform with volume charge density ρ = Q/V, Q is the total charge and V is the total volume. Above integral can be written as
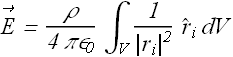
In three dimensions, we need to compute three integrals, one for each component.
Checkpoint 3 (Electric Field due to a line charge)
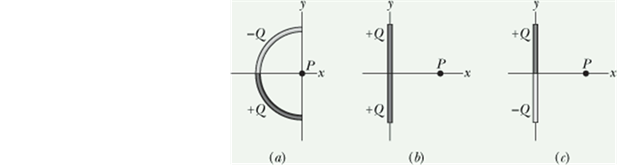
The figure here shows three nonconducting rods, one circular and two straight. Each has a uniform charge of magnitude Q along its top half and another along its bottom half.
For each rod, what is the direction of the net electric field at point P?
Electric field of a uniformly charged ring
To compute electric field at a point P on the axis passing through the center of a uniformly charged ring of radius R, we can divide the ring in equal segments of length ds.
Let us assume that λ is the linear charge density of the ring.
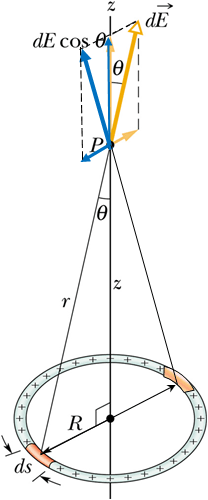
The electric field ![]() generated by element ds has two components, one parallel to z-axis and other perpendicular to z-axis.
generated by element ds has two components, one parallel to z-axis and other perpendicular to z-axis.
Due to the presence of identical element on diagonally opposite side, the perpendicular components get canceled.
Total electric field is due to the addition of z-components of each element.
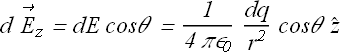
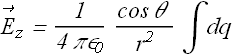
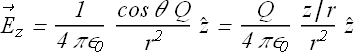
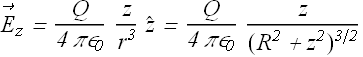
Electric Field of a Charged Disk
Consider a uniformly charged disk of radius R with surface charge density σ.
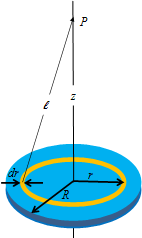
Since it is a disk so let us consider its surface charge density ![]() .
.
We have already calculated the electric field at point P due to a ring.
Let us consider a ring of width dr, radius r. Total charge on the ring of area dA will be
![]()
The electric field dE generated by this ring along z-axis is
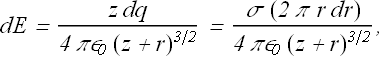
Total electric field is computed by integration
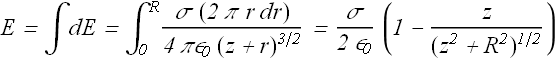
Electric Field of an infinite sheet
Electric field of a uniformly charged disk with σ surface charge density is given as

What if the radius R→∞? The disk becomes an infinite sheet.
Electric field for such a sheet will be
![]()
Similarly for a finite sheet if we want to compute electric field very close to the sheet then we can assume z<<R.
In such situation we again get
![]()
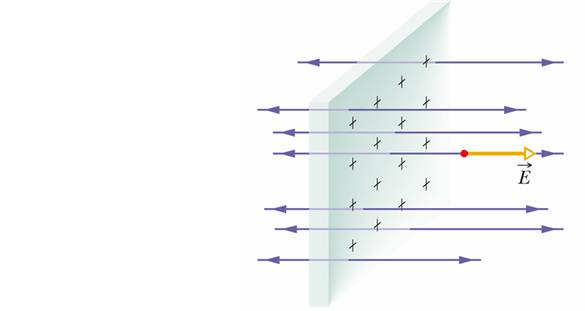
Is Electric Field Real?
Simple reason for us to introduce the concept of Electric field was:
Once we know the electric field ![]() at some location, we know the electric force
at some location, we know the electric force ![]() acting on any charge q that we place there.
acting on any charge q that we place there.
Electric field is a kind of "invisible influence" of a charge or charges at different locations in space, which can be experienced by other charge or charges.
However, Einstein's special theory of relativity predicts that nothing can move faster than the speed of light ![]() /s), therefore influence of a charge (Electric field) too can not move faster than this speed.
/s), therefore influence of a charge (Electric field) too can not move faster than this speed.
With the assumption of finite speed of electric field let us watch its behavior with time in following simulations.
Create a charge at a location and watch how the "invisible influence" (electric field) travels with time.
Now destroy this charge and see how the electric field gets wiped out with time?
You can see that even after the destruction of charge, its electric field exists for finite time at various locations of space.
This shows that Electric Field concept is necessary to explain this phenomenon.
Electric Field of a charge exists even after destruction of the charge.
Electric Dipole in a Uniform Electric Field
Net Force
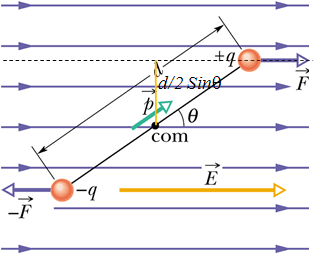
Consider an electric dipole in uniform electric field ![]() . Let us see if it is in equilibrium or not?
. Let us see if it is in equilibrium or not?
First we calculate net force ![]() on the dipole.
on the dipole.
Force on the negative charge is ![]() and is given as
and is given as
![]()
Similarly force on the positive charge will be ![]()
![]()
![]()
This shows net force on the dipole is zero.
Net Torque
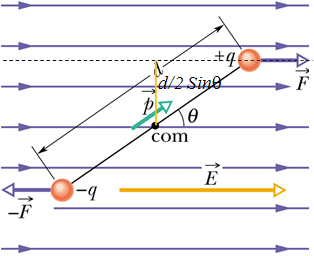
Now let us calculate net torque ![]() on the dipole First calculate torque
on the dipole First calculate torque ![]() on the negative charge.
on the negative charge.
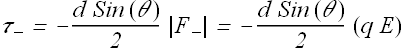
Minus sign indicates that rotation is clockwise.
Now let us calculate torque ![]() on the positive charge.
on the positive charge.
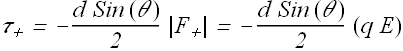
![]() again produce rotation in clockwise direction.
again produce rotation in clockwise direction.
Net torque ![]() is
is
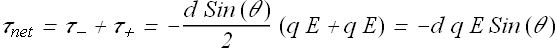
![]()
We can write net torque acting on the dipole in terms of dipole moment
![]()
In vector Notation we can write
![]()
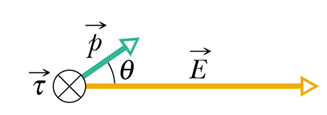
Electric dipole in a uniform field can not move but it can rotate.
Behavior of a water molecule in electric field.
Click PLAY to put the electric field on. PAUSE and then use RESET button to put it off.
Potential Energy of an Electric Dipole in a Uniform Electric Field
Suppose an electric dipole rotate by an angle θ in an electric field ![]() . The change in potential energy ΔU of the dipole will be
. The change in potential energy ΔU of the dipole will be
![]()
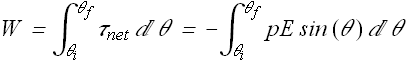
![]()
![]()
Stable equilibrium point of a dipole :
When a dipole makes 0° angle with electric field, its potential energy is minimum.
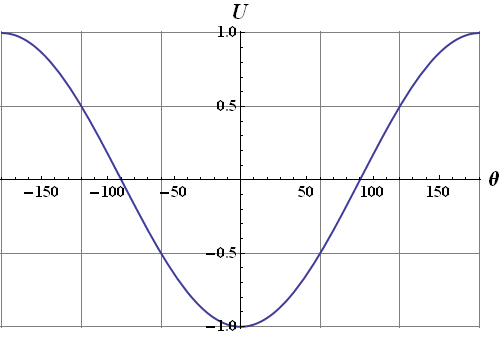
Variation of dipole potential energy with angle θ.
For a dipole in electric field 0° is a stable equilibrium point
Unstable equilibrium point of a dipole :
When a dipole makes 180° angle with electric field, its potential energy is maximum.
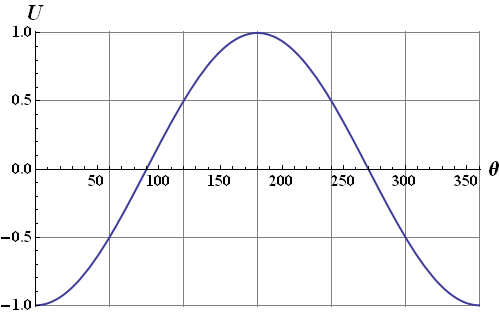
Variation of dipole potential energy with angle θ.
For a dipole in electric field 180° is an unstable equilibrium point
Simulation of a dipole in a uniform electric field
Change initial angle θ between dipole moment ![]() and electric field
and electric field ![]() to zero and apply electric field (Click PLAY).
to zero and apply electric field (Click PLAY).
Watch the dipole, it is in its stable equilibrium position (Minimum energy position) so nothing happens.
Now change the angle to a different value and watch the motion (Click PAUSE, RESET and PLAY again).
Change initial angle θ between dipole moment ![]() and electric field
and electric field ![]() to 180° and apply electric field (Click PAUSE, RESET and PLAY again).
to 180° and apply electric field (Click PAUSE, RESET and PLAY again).
Watch the dipole in its unstable equilibrium position (Maximum energy position) , again nothing happens.
Now change the angle by small value and watch the motion (Click PAUSE, RESET and PLAY again).
Dipole returns back to its stable equilibrium position.
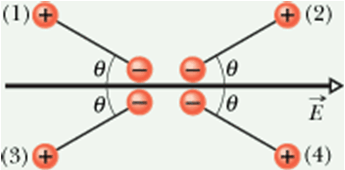
Checkpoint 4 (Electric Dipole)
The figure shows four orientations of an electric dipole in an external electric field. Rank the orientations according to
(a) the magnitude of the torque on the dipole and
(b) the potential energy of the dipole, greatest first.