Diffraction
No one has ever been able to define the difference between interference and diffraction satisfactorily.
There is no specific, important physical difference between the two.
When there are only a few interfering sources, say two, then the result is usually called Interference.
If there are larger number of sources, word Diffraction is more often used.
Objectives
In this chapter we will learn following topics.
Fresnel Bright Spot.
Amplitude due to interference of n equal light (electromagnetic wave) sources.
Diffraction by a single slit.
Basic concept of diffraction grating.
Fresnel Bright Spot
Diffraction can only be explained by wave theory of light.
Huygens proposed wave theory in 1600s.
Newton's theory was that light is a stream of particles.
Even in 1819, scientific circles were dominated by Newton's supporters. To challenge wave theory, they arranged an assay competition.
Augustin Fresnel presented his experiments on light and his wave theory explanation of those experiments.
One of the Newton's supporter S. D. Poisson, pointed out that if Fresnel's explanation is correct, then in the center of the shadow of a opaque sphere or disk, there should be a bright spot.
Competition committee arranged an experiment to verify this prediction.
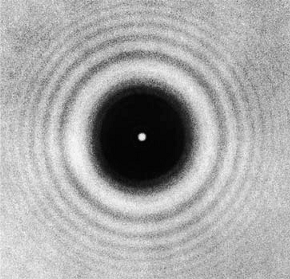
To the surprise of every one Poisson's prediction indeed turns out to be true.
This bright spot is called Fresnel bright spot.
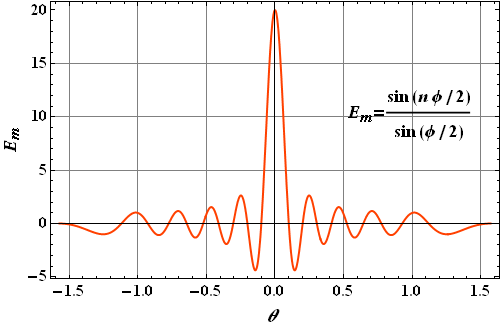
Amplitude due to n equal oscillators
Let us consider n equally spaced oscillators, all of equal amplitude E, but different from one another in phase as shown
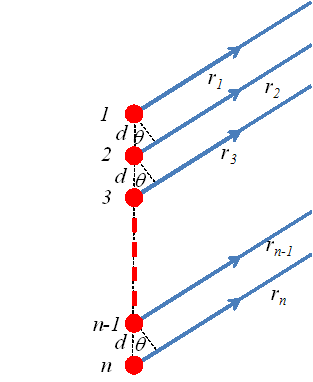
![]()
If we are observing in a given direction θ, the phase term φ can be computed from the path difference.
![]()
Where α is the initial constant phase.
These all terms can be added geometrically using phasor diagram.
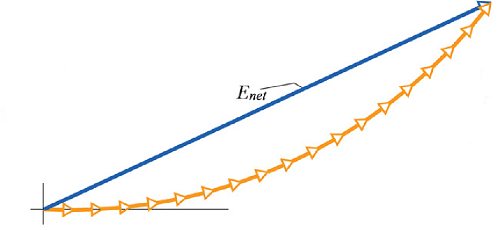
Using this technique ![]() turns out to be
turns out to be

Intensity at any point is proportional to energy density, therefore intensity in a given direction θ is
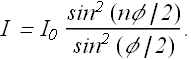
 |
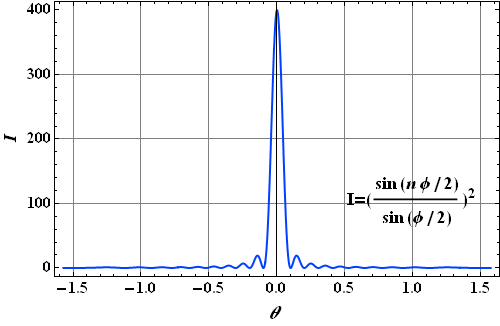 |
Diffraction by a single slit
Let us now examine the diffraction pattern of a plane wave of light of wavelength λ through a narrow slit of width a.
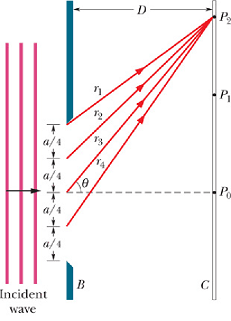
According to Huygens' principle, we can divide the slit in n equidistant point sources.
The distance between each source d=a/n.
According to our formula for n interfering sources, Intensity at any point in a given direction θ is
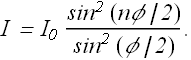
with φ in this case is
![]()
Here we have assumed that initial constant phase α=0.
Intensity in a given direction θ can be rewritten as
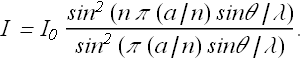
In the first place there will be maxima when φ=π (a/n) sinθ/λ=0. That means that all the oscillators are in phase and there is a strong intensity in the direction θ=0.
Where will be first minima?
Let us first look at the plot of sin(nφ/2) and sin(φ/2) as a function of θ.
![]()
and
![]()
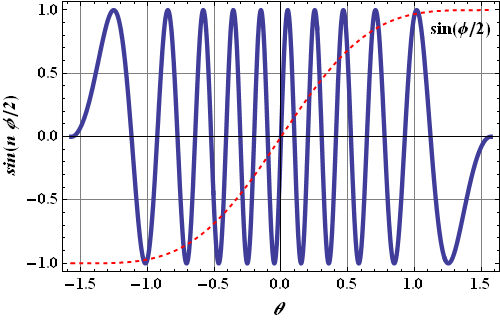
We can see the term sin(nφ/2) (blue) is changing faster than term sin(φ/2) (dashed red).
First minima will be where term sin(nφ/2) will have first minima or when n φ/2=π
![]()
or
![]()
Here n d=a the slit width, therefore we can say first minima occurs at
![]()
Similarly second minima will occur at
![]()
Or dark fringes will occur at
![]()
Here you can see that a sinθ is the path length difference between the top and the bottom ray.
Checkpoint 1
We produce a diffraction pattern on a viewing screen by means of a long narrow slit illuminated by blue light. Does the pattern expand away from the bright center (the maxima and minima shift away from the center) or contract toward it if we (a) switch to yellow light or (b) decrease the slit width?
Hint : (a) If we switch to yellow, wavelength λ increases, that means product a sin θ should increase, a is fixed so θ should increase.
(b) When a decreases, to keep product a sin θ constant, we should increase θ.
Diffraction grating
Suppose we had a lot of parallel conducting wires, equally spaced at a spacing d.
Suppose we have a electromagnetic wave source far away, practically at infinity.
This external electric field will drive the free charges in conductors, up and down (oscillate the free electrons in conducting wires).
These wires will become secondary sources of electromagnetic waves as charges are oscillating.
This phenomenon is called scattering.
This can also be done with light waves, we use a flat piece of glass or a metal and make notches in it in such a way that each notch scatter light different than the rest of the block.
Suppose light is hitting the surface from an angle ![]() .
.
We are observing the scattered light due to all the notches at an angle ![]() .
.
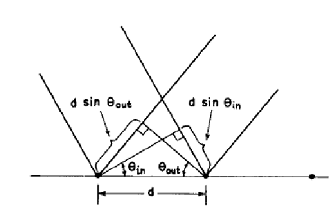
In this situation we will get phase difference φ in each notch as
![]()
For intensity due to n sources we again use the formula

For intensity will be maximum when φ is a multiple of 2π.
First maxima will be when φ=0, means when ![]() . This is called first order of the grating.
. This is called first order of the grating.
When ![]() , the other maxima will occur when ever
, the other maxima will occur when ever
![]()
m=1, will be second order line and so on.
