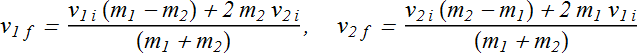Center of Mass and Linear Momentum
Objectives
In this chapter we will learn the following concepts:
Center of mass (com) for a system of particles.
How to calculate center of mass of a continuous object.
How to apply Newton’s Second law to a system of particles.
Linear momentum for a single particle and a system of particles.
Impulse and its relation to change in momentum.
The principle of conservation of linear momentum.
We will use the conservation of linear momentum to study collisions in one and two dimensions.
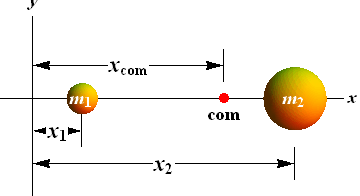
Center of Mass
The center of mass (com) of a system of particles is the point that moves as though (1) all of the system’s mass were concentrated there and (2) all external forces were applied there.
Consider a system of two particles of masses ![]() and
and ![]() at positions
at positions ![]() and
and ![]() respectively. Position of center of mass
respectively. Position of center of mass ![]() of this system is defined as
of this system is defined as
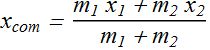
Center of mass for many particles
If there are n particles, the center of mass of these n particles will be
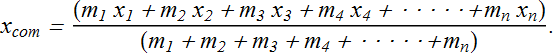
Total mass M of n particles is
![]()
Therefore center of mass of n particles can also be written as
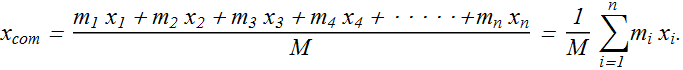
How to calculate Center of Mass in 3D?
We can calculate three position coordinates ![]() separately in three dimensions.
separately in three dimensions.

Here ![]() are the position coordinates for i th particle.
are the position coordinates for i th particle.
![]()
Similarly position vector ![]() of center of mass can be written as
of center of mass can be written as
![]()
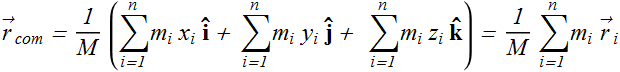
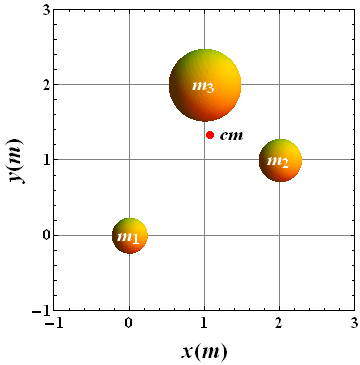
Example 1: Center of Mass
Following figure shows a three-particle system, with masses ![]() ,
, ![]() and
and ![]() . The scales on the axes are set by
. The scales on the axes are set by ![]() and
and ![]() .
.
What are (a) the x coordinate and (b) the y coordinate of the system’s center of mass? (c) If ![]() is gradually increased, does the center of mass of the system shift toward or away from that particle, or does it remain stationary?
is gradually increased, does the center of mass of the system shift toward or away from that particle, or does it remain stationary?

How to calculate Center of Mass in Solid Objects?
We can assume that solid object is made up of n small elements of mass Δm each.

Let us consider, ![]() is the position vector of ith element of the object.
is the position vector of ith element of the object.
Coordinates of center of mass of such a solid object can be written as
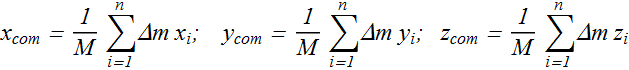
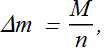
When we make these elements extremely small such that n→∞, in that case Δm→0 and summation becomes integral.
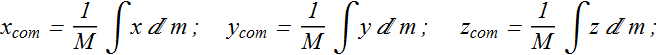
When the density ρ of the object is uniform, the mass and volume at all the positions in the object can be given as
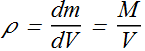
Where dV is the volume of small element of mass dm and V is total volume of the object.
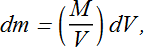
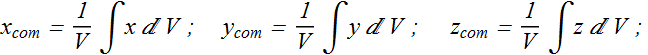
Symmetric Objects
These integrals can be avoided if the object has a point, a line or a plane of symmetry.
The center of mass of such an object then lies at that point, on that line, or in that plane.
Examples:
The center of mass of a uniform sphere (which has a point of symmetry) is at the center of the sphere.
The center of mass of a uniform cuboid (which has planes of symmetry) is at the center of the intersection of two diagonals as shown.
 |
 |
The center of mass of a uniform rectangular object lies at the intersection of the diagonals.
The center of mass of a banana (which has a plane of symmetry that splits it into two equal parts) lies somewhere in that plane.
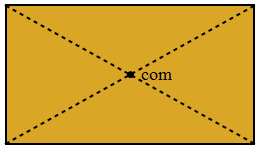
The center of mass of an object need not lie within the object. There is no dough at the com of a dough-nut, and no iron at the com of a horseshoe.
Checkpoint-1: Center of Mass
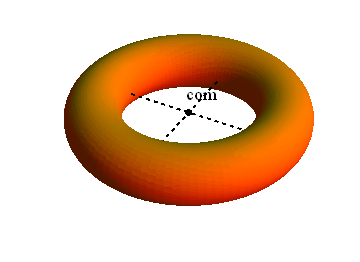
The figure shows a uniform square plate from which four identical squares at the corners will be removed.
(a) Where is the center of mass of the plate originally?
Where is it after the removal of (b) square 1; (c) squares 1 and 2; (d) squares 1 and 3; (e) squares 1, 2, and 3; (f) all four squares? Answer in terms of quadrants, axes, or points (without calculation, of course).
Newton’s Second Law for a system of Particles
Consider multi-particle system comprises of n particles.
We are not interested in the individual motions of these particles.
We are only interested in the motion of the center of mass ![]() of this multi-particle system.
of this multi-particle system.
According to Newton’s second law
![]()
![]() is the net external force acting on this multi-particle system.
is the net external force acting on this multi-particle system.
M is the total mass of the system and ![]() is the acceleration of the center of mass of the system.
is the acceleration of the center of mass of the system.
Components of net external force are related to components of acceleration of center of mass.
![]()
Checkpoint-2: Newton’s Second law
Two skaters on frictionless ice hold opposite ends of a pole of negligible mass. An axis runs along the pole, and the origin of the axis is at the center of mass of the two-skater system. One skater, Fred, weighs twice as much as the other skater, Ethel.
Where do the skaters meet if
(a) Fred pulls hand over hand along the pole so as to draw himself to Ethel,
(b) Ethel pulls hand over hand to draw herself to Fred, and
(c) both skaters pull hand over hand?
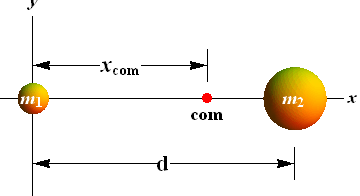
Example 2: Newton’s Second law
Two skaters, one with mass 65 kg and the other with mass 40 kg, stand on an ice rink holding a pole of length 10 m and negligible mass. Starting from the ends of the pole, the skaters pull themselves along the pole until they meet.
How far does the 40 kg skater move?
Hint :
Linear Momentum
The linear momentum of a particle ![]() is defined as
is defined as
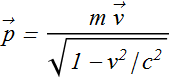
m is the mass of the particle and ![]() is its velocity and
is its velocity and ![]() is the speed of light.
is the speed of light.
For slow moving objects (v<<c), the approximate expression for momentum is given as
![]()
Since m is a scalar quantity and velocity ![]() is a vector quantity, therefore linear momentum
is a vector quantity, therefore linear momentum ![]() is a vector.
is a vector.
As m is always positive, therefore ![]() and
and ![]() have the same direction.
have the same direction.
The SI unit for linear momentum is the kilogram-meter per second (kg · m/s).
![]()
Relation between Linear Momentum and Force.
As per Newton's Law we know that
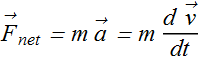
When mass of a particle remains constant we can rewrite it as
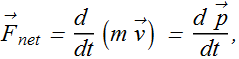
The time rate of change of the momentum of a particle is equal to the net external force acting on the particle and is in the direction of that force.
This relation between net force and momentum is always valid (whether the mass is constant or changes with time).
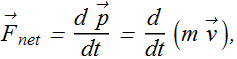
Differentiation by parts give us
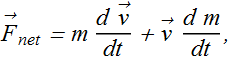
This is the complete expression of "Newton's second law".
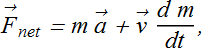
If mass m of the particle is constant with time, then
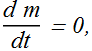
![]()
Checkpoint-3: Linear Momentum
The figure gives the magnitude p of the linear momentum versus time t for a particle moving along an axis. A force directed along the axis acts on the particle.
(a) Rank the four regions indicated according to the magnitude of the force, greatest first.
(b) In which region is the particle slowing?
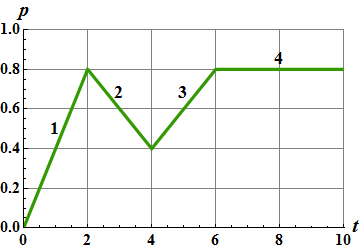
Hint :
The Linear Momentum of a system of Particles
Consider a system of n particles, each with its own mass, velocity, and linear momentum.
The system as a whole has a total linear momentum ![]() , which is the vector sum
of linear momentum of the each individual particle.
, which is the vector sum
of linear momentum of the each individual particle.
![]()
We can also write total linear momentum ![]() as
as
![]()
Total Linear Momentum and velocity of center of mass
Velocity of center of mass of a multi-particle system is written as
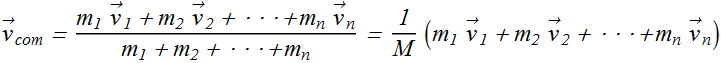
Where M is the total mass of the system.
If we compare the above two equations, total linear momentum ![]() of a multi-particle system can be written as
of a multi-particle system can be written as
![]()
The linear momentum of a system of particles is equal to the product of the total mass M of the system and the velocity of the center of mass.
Example 3: Linear Momentum
A 0.70 kg ball moving horizontally at 5.0 m/s strikes a vertical wall and rebounds with speed 2.0 m/s.
What is the magnitude of the change in its linear momentum?
Solution :
Initial momentum ![]() is
is
![]()
Final momentum ![]() is
is
![]()
Therefore change in momentum is
![]()
![]()
![]()
Impulse
When a constant acceleration is applied to an object from time ![]() to
to ![]() , as per kinematic equations the relation between its initial
, as per kinematic equations the relation between its initial ![]() and final
and final ![]() velocity is given as
velocity is given as
![]()
Multiply both sides by mass m of the object.
![]()
Left hand side is change in momentum ![]() , of the object and right hand side is the product of force and time duration Δt of its action.
, of the object and right hand side is the product of force and time duration Δt of its action.
![]()
![]() is also known as impulse. Symbol
is also known as impulse. Symbol ![]() is used for impulse.
is used for impulse.
![]()
What if force is not constant?
We can divide time in small interval and calculate impulse in each interval, sum of impulses will give us net change in momentum.
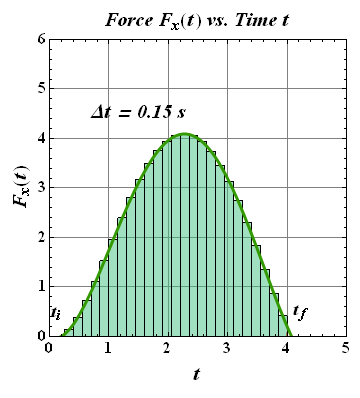
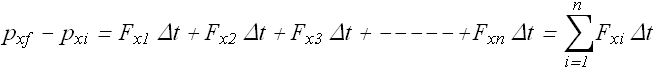
When Δt→0, above summation gets converted into integral from initial time ![]() to final time
to final time ![]() .
.
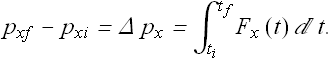
The right side of above equation is the impulse.
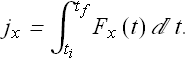
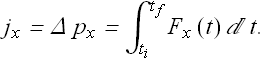
Computation of average force from change in momentum.
In most of the practical situations force is not constant during its time of action.
Variation of force with time is also not known.
In such situations, it is not easy to calculate impulse as an integral.
Example :
Consider a collision of a "baseball bat" and "ball".
Here bat exerts force on the ball and ball exerts force on the bat.
It is easy to measure start time ![]() when the ball touches the bat and ends time
when the ball touches the bat and ends time ![]() when the two object separate.
when the two object separate.
The momentum of the ball is changing during this time interval.
Suppose force F(t) at the time of collision, acting on the ball, is known as a function of time t. We can compute the impulse j along acting on the ball.
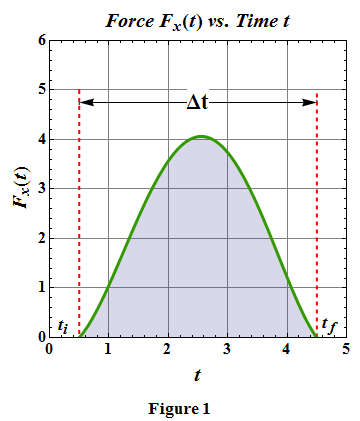
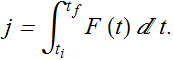
This indicates, impulse j is the area under the curve shown in Fig. 1.
In majority of the cases we do not know functional form of force F(t), therefore we can not compute impulse by this method.
But we can always measure initial momentum ![]() and final momentum
and final momentum ![]() the ball.
the ball.
Therefore change in momentum ![]() is given as
is given as
![]()
Impulse can be estimated from the change in momentum Δp.
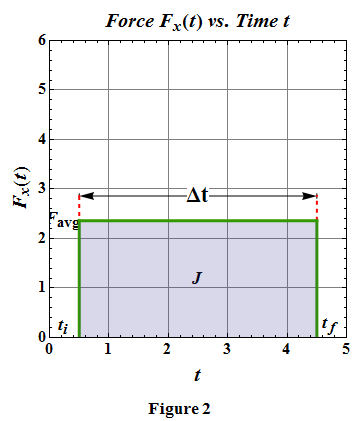
Can we compute average force ![]() acting on the ball from the measured impulse?
acting on the ball from the measured impulse?
Answer is YES.
We can assume a constant average force ![]() acting on the ball during collision interval
acting on the ball during collision interval ![]() .
.
In terms of constant average force ![]() , the magnitude of impulse
, the magnitude of impulse ![]() can be written as
can be written as
![]()
Therefore average force acting on the ball can be estimated by dividing change in momentum Δp with time interval Δt.
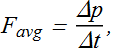
In graphical terms, value of the magnitude of average force ![]() will be such that area under the curve in Fig. 2 is same as in Fig. 1.
will be such that area under the curve in Fig. 2 is same as in Fig. 1.
Checkpoint-4: Collisions and Impulse
A paratrooper whose chute fails to open lands in snow; he is hurt slightly. Had he landed on bare ground, the stopping time would have been 10 times shorter and the collision lethal.
Does the presence of the snow increase, decrease, or leave unchanged the values of
(a) the paratrooper’s change in momentum,
(b) the impulse stopping the paratrooper, and
(c) the force stopping the paratrooper?
Checkpoint-5: Collisions and Impulse
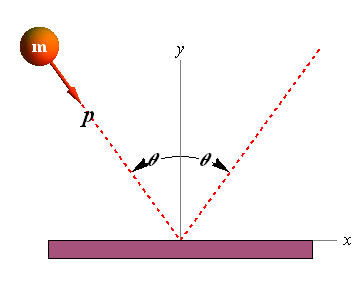
The figure shows an overhead view of a ball bouncing from a vertical wall without any change in its speed. Consider the change ![]() in the ball’s linear momentum.
in the ball’s linear momentum.
(a) Is ![]() positive, negative, or zero?
positive, negative, or zero?
(b) Is ![]() positive, negative, or zero?
positive, negative, or zero?
(c) What is the direction of ![]() ?
?
Example 3: (Collisions and Impulse)
In a common but dangerous prank, a chair is pulled away as a person is moving downward to sit on it, causing the victim to land hard on the floor. Suppose the victim falls by 0.50 m, the mass that moves downward is 70 kg, and the collision on the floor lasts 0.082 s.
What are the magnitudes of the (a) impulse and (b) average force acting on the victim from the floor during the collision?
Solution :
First we need to calculate velocity of the person just before the collision
![]()
Initial kinetic energy is zero, if v is the final velocity then
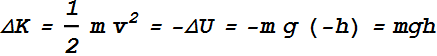
Therefore magnitude of v is
![]()
Now initial momentum ![]() is
is
![]()
Since final momentum ![]() , therefore
, therefore
![]()
(a) Magnitude of impulse ![]() .
.
![]()
![]()
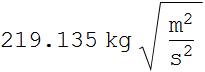
(a) Average force ![]() .
.
![]()
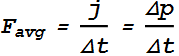
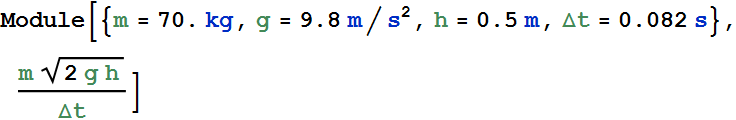

Conservation of Linear Momentum
We know that in the presence of net external force ![]() , the time rate of change of momentum is given as
, the time rate of change of momentum is given as
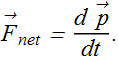
If no external force is present, ![]() , in that case
, in that case
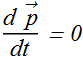
Or
![]()
This means final momentum will be equal to the initial momentum.
If no net external force acts on a system of particles, the total linear momentum of the system cannot change.
This result is called the law of conservation of linear momentum.
If only one component of the external force is zero, say ![]() , in that case only x component
, in that case only x component ![]() of the momentum will be constant.
of the momentum will be constant.
![]()
Or
![]()
If the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum of the system along that axis cannot change.
Example 5: Conservation of Linear Momentum
A 91 kg man lying on a surface of negligible friction shoves a 68 g stone away from himself, giving it a speed of 4.0 m/s.
What speed does the man acquire as a result?
Solution :
Checkpoint-6: Conservation of linear Momentum
An initially stationary device lying on a frictionless floor explodes into two pieces, which then slide across the floor. One piece slides in the positive direction of an x axis. (a) What is the sum of the momenta of the two pieces after the explosion? (b) Can the second piece move at an angle to the x axis? (c) What is the direction of the momentum of the second piece?
Different types of collisions
In the absence of any external force, linear momentum is always conserved regardless of the collision type.
Elastic Collision:
When two or more objects collide in the absence of any external force, linear momentum of the system is conserved and collision is elastic if kinetic energy of the system is also conserved.
![]()
In an elastic collision, the kinetic energy of each colliding body may change, but the total kinetic energy of the system does not change.
Inelastic Collision:
When two or more objects collide in the absence of any external force, linear momentum of the system is conserved and collision is inelastic if kinetic energy of the system is not conserved.
![]()
Checkpoint-6: Inelastic Collision
Body 1 and body 2 are in a completely inelastic one-dimensional collision. What is their final momentum if their initial momenta are, respectively, (a) 10 kg·m/s and 0; (b) 10 kg·m/s and 4 kg·m/s; (c) 10 kg·m/s and -4 kg·m/s
Checkpoint-7: Elastic Collision
What is the final linear momentum of the target (green sphere) in following figure, if the initial linear momentum of the projectile (orange sphere) is 6 kg·m/s and the final linear momentum of the projectile is (a) 2 kg·m/s and (b) −2 kg·m/s? (c) What is the final kinetic energy of the target if the initial and final kinetic energies of the projectile are, respectively, 5 J and 2 J?
(a)
(b)
Checkpoint-8: Two dimensional Collision
In following figure, suppose that the projectile has an initial momentum of 6 kg·m/s, a final x component of momentum of 4 kg·m/s, and a final y-component of momentum of −3 kg·m/s. For the target, what then are (a) the final x component of momentum and (b) the final y component of momentum?
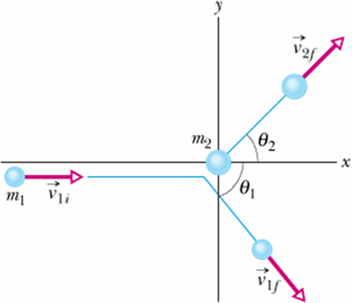
Examples of Elastic and Inelastic Collisions :
For elastic collision Kinetic energy of the system is conserved.
![]()
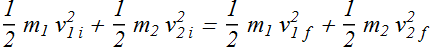
Momentum is also conserved.
![]()
![]()
When we solve above two equations we can get the values of final velocities ![]() of both particles in terms of initial velocities
of both particles in terms of initial velocities ![]() and masses
and masses ![]() .
.