Electric Potential
Objectives
In this chapter we will define the electric potential ( symbol V ) associated with the electric force and accomplish the following tasks:
Calculate V if we know the corresponding electric field.
Calculate the electric field if we know the corresponding potential V.
Determine the potential V generated by a point charge.
Determine the potential V generated by a discrete charge distribution.
Determine the potential V generated by a continuous charge distribution.
Determine the electric potential energy U of a system of charges.
Define the notion of an equipotential surface.
Explore the geometric relationship between equipotential surfaces and electric field lines.
Explore the potential of a charged isolated conductor.
Electric Potential Energy
Points to Remember
Concept of potential energy is used in conservative forces.
Electrostatic force is a conservative force.
The potential energy is always associated with a system of two or more particles.
The work done by a conservative force is independent of path.
Change in Potential Energy of a moving particle:
Consider an object moving under the influence of a force ![]() . If the object moves from an initial position i to a final position f , the change in potential energy ΔU is given as
. If the object moves from an initial position i to a final position f , the change in potential energy ΔU is given as
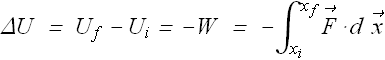
Change in Potential Energy of a charge moving in an electric field:
Consider an electric charge ![]() moving from an initial position i to a final position f under the influence of an electric field
moving from an initial position i to a final position f under the influence of an electric field ![]() .
.
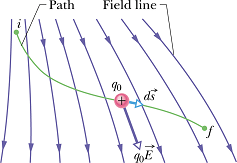
The force exerted on the charge will be
![]()
Change in potential energy for moving charge ![]() from position i to f will be
from position i to f will be
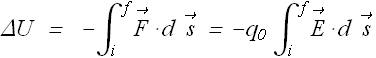
Problem 1
Checkpoint 1
In the figure, a proton moves from point i to point f in a uniform electric field directed as shown. (a) Does the electric field do positive or negative work on the proton? (b) Does the electric potential energy of the proton increase or decrease?

Solution
![]()
Since q is positive (proton charge) the work done is negative
![]()
Positive change in potential energy means the potential energy of proton increases.
Electric Potential
The electric potential energy depends on the charge q. A new quantity named "Electric potential" is defined which is independent of charge.
Change in "Electric potential" ΔV is defined as
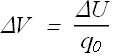
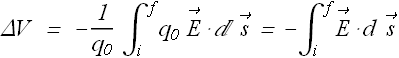
Like potential energy, in all physical problems only the change in electric potential ΔV is involved.
Thus electric potential at any arbitrary point can be defined as a reference value.
We choose that reference point to be infinity and choose the value of electric potential to be zero at infinity.
With infinity as reference point the electric potential ![]() at any point P can be given as
at any point P can be given as
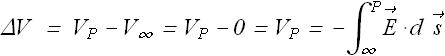
Electric potential only depends on the coordinates of point P, and electric field ![]() .
.
SI units for electric potential is "J/C" and it is called "Volts"
"Electric potential " is a scalar property associated with an electric field, regardless of whether a charged object has been placed in that field; it is measured in joules per coulomb, or volts.
"Electric potential energy" is an energy of a charged object in an external electric field (or more precisely, an energy of the system consisting of the object and the external electric field); it is measured in joules.
Checkpoint 2
In the figure below, we move the proton from point i to point f in a uniform electric field directed as shown. Does the proton move to a point of higher or lower potential?
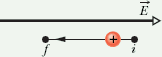
Solution
![]()
![]()
Calculating the potential from the electric field
Problem - 2 (How to calculate electric potential from Electric field)
The electric field in a region of space has the components ![]() and
and ![]() . Point A is on the y axis at y = 2.40 m, and Point B is on the x axis at x = 3.00 m. What is the potential difference
. Point A is on the y axis at y = 2.40 m, and Point B is on the x axis at x = 3.00 m. What is the potential difference ![]() ?
?
![]()
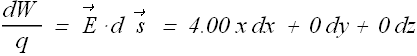
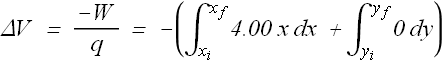
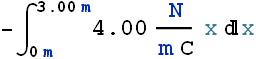
Equipotential Surfaces
A collection of points that have the sam "electric potential" is known as an equipotential surface. Four such surfaces are shown in the figure.
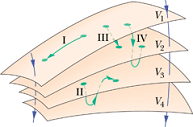
If ΔV is the potential difference between two points, the work done W by electric field will be
![]()
For Path I the work done ![]() , because ΔV = 0.
, because ΔV = 0.
For Path II the work done ![]() , because ΔV = 0.
, because ΔV = 0.
For Path III the work done ![]() .
.
For Path IV the work done ![]() .
.
When a charge move on an equipotential surface, the change in potential ΔV =0, therefore the work done by an electric field is zero.
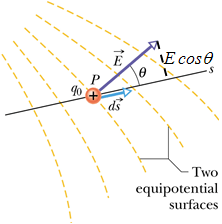
Show that Electric field ![]() is always perpendicular to the equipotential surface :
is always perpendicular to the equipotential surface :
Let us assume that a charge q moves from point A to point B on an equipotential surface in the influence of an electric field ![]() with displacement
with displacement ![]() .
.
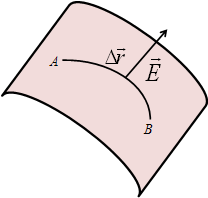
The work done by field will be given as
![]()
In terms of potential difference W is given as
![]()
Or we can say that on an equipotential surface
![]()
Here θ is the angle between ![]() and
and ![]() , for above equation to be true
, for above equation to be true
![]()
That means the angle θ between the electric field ![]() and the displacement
and the displacement ![]() will be 90° at all the points on an equipotential surface.
will be 90° at all the points on an equipotential surface.
This is true for any path on the equipotential surface.
Therefore electric field is always perpendicular to the equipotential surface.
Examples of Equipotential Surfaces :
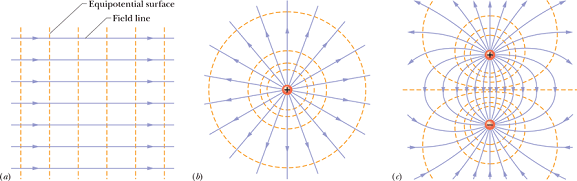
Figure: (a) Uniform Electric Field (b) A point charge (c) A dipole
For a point charge, the equipotential surfaces are concentric spheres.
Problem 3
An infinite nonconducting sheet has a surface charge density = 0.10 ![]() on one side. How far apart are equipotential surfaces whose potentials differ by 88 V?.
on one side. How far apart are equipotential surfaces whose potentials differ by 88 V?.
Change in potential energy ΔV is related to the electric field ![]() as
as
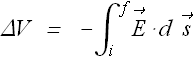
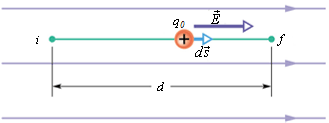
Imagine that a test charge ![]() moves from initial position i to a final position f.
moves from initial position i to a final position f.
Electric field is a conservative force so the work done for moving the charge from i to f is independent of path.
Choose a path that is parallel to the electric field.
![]()
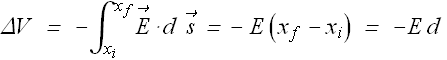
Electric field due to an infinite sheet is always perpendicular to the sheet surface and its magnitude is related to the charge density σ
![]()
![]()
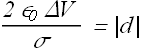
The change in potential ΔV from i to f is negative.
Checkpoint 3
The figure here shows a family of parallel equipotential surfaces (in cross section) and five paths along which we shall move an electron from one surface to another. (a) What is the direction of the electric field associated with the surfaces? (b) For each path, is the work we do positive, negative, or zero? (c) Rank the paths according to the work we do, greatest first.
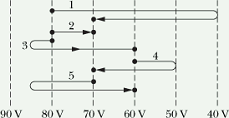
Electric field is always perpendicular to the equipotential surfaces.
The direction of field will be along x axis. Let us check if it will be negative or positive.
(1)
Along path 1
![]()
ΔV is negative.
![]()
Since ![]() is parallel to
is parallel to ![]() , therefore θ should be either 0° or 180°.
, therefore θ should be either 0° or 180°.
But for ΔV to be negative, Cos(θ) = 1 → θ = 0°.
Electric field is along positive x direction.
(2)
Along path 2 and path 1
![]()
Since q is negative, work done W by electric field is negative, therefore we have done a positive work.
(3)
Along path 3
![]()
Since q is negative, work done W by electric field is negative, therefore we have done a positive work.
(4)
Along path 4
![]()
Since q is negative, work done W by electric field is positive, therefore we have done a negative work.
(5)
Along path 5
![]()
Since q is negative, work done W by electric field is negative, therefore we have done a positive work.
Potential Due to a Point Charge
If we know electric potential at a point due to a "point charge", we can calculate potential due to many point charges or even due to charged objects.
Consider a point charge q placed at the origin.
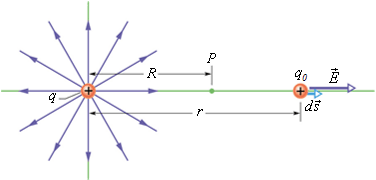
The potential ![]() at point P is givens
at point P is givens
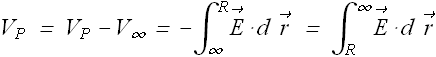
We have already defined that ![]() .
.
Now the electric field at a distance r from the point charge q is given as
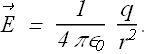
The value of ![]() will be given as
will be given as
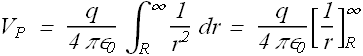
![]()
A positively charged particle produces a positive electric potential. A negatively charged particle produces a negative electric potential.
Potential Due to a Group of Point Charges
Electric potential is a scalar quantity.
Electric potential ![]() due to i th point charge is
due to i th point charge is

Total potential V at a point P is an algebraic sum of individual electric potentials due to all n charges.
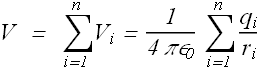
Checkpoint 4
The figure here shows three arrangements of two protons. Rank the arrangements according to the net electric potential produced at point P by the protons, greatest first.

(a)
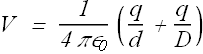
(b)
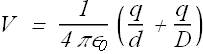
(c)
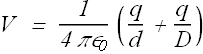
Electric potential in all the cases is equal.
Electric field at P in all the three cases will be different.
Checkpoint 5
Four protons are equally spaced around a circle. If we make these protons unequally spaced, (a) will the electric potential at point P change? (b) Will the "electric field" at point P change?
(Click hold and drag any charge to move and see if electric potential in the meter changes and how the electric field at point P changes)
Checkpoint 5
Four protons are equally spaced around a circle. If we change the radius of the circle (a) will the electric potential at point P change? (b) Will the electric field at point P change?
(Click hold and drag the slider to change radius of circle and see if electric potential in the meter changes and how the electric field at point P changes)
Problem 4 (How to calculate Electric potential due to a group of charges)
In the figure below, particles of charge ![]() and
and ![]() are fixed in place with a separation of d = 38.0 cm. With V = 0 at infinity, at what finite values of x is the net electric potential on the x-axis also zero?
are fixed in place with a separation of d = 38.0 cm. With V = 0 at infinity, at what finite values of x is the net electric potential on the x-axis also zero?
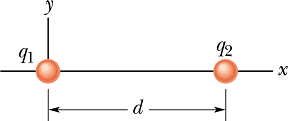
Let us assume charge ![]() is placed at origin.
is placed at origin.
Consider point P on +x axis.
The electric potential due to two charges will be will be given as (Magnitude of the distance is taken)
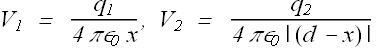
Total potential will be sum of these two potential
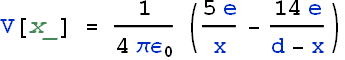
Magnitude of x
![]()
![]()
Let us assume charge ![]() is placed at origin.
is placed at origin.
Consider point P on -x axis.
The electric potential due to two charges will be will be given as (Magnitude of the distance is taken)
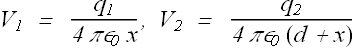
Total potential will be sum of these two potential
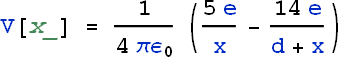
Magnitude of x
![]()
![]()
Potential Due to a Continuous Charge Distribution
Divide the charge distribution into small elements.
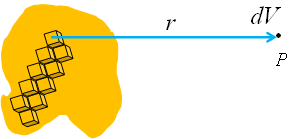
Treat each element as a point charge.
Calculate electric potential dV due to each element at point P.
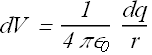
Sum these individual electric potentials to get total potential V at P
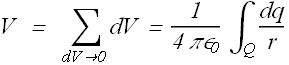
Line of Charge
Consider a line charge of length L and linear charge density λ.
Divide this length into small segments of length dx.
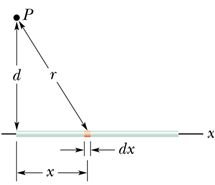
Consider one such element at a distancex from the origin.
Charge on this element will be dq = λ dx . The electric potential dv due to this element at P will be
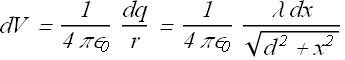
Here we have used the relation ![]() .
.
Total electric potential V at P will be
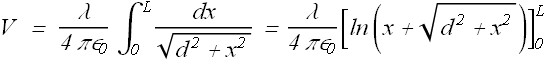
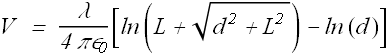
Charged Disk
Consider a uniformly charged disk of radius R with surface charge density σ.
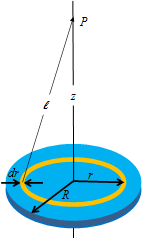
Let us calculate electric potential V(z) at a point P on the central axis at a distance z from the disk center.
First divide the disk into flat rings of width dr. Let us consider one of the ring of radius r, and calculate potential at point P due to this ring.
Since all the charges on this ring are at a distance ℓ, from the point P, therefore the potential due to the total charge dq, on this ring is
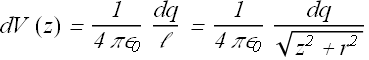
Area of the ring is (2π r)dr , therefore total charge dq = σ (2πr)dr. Now dV(z) is given as
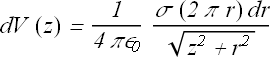
Total potential due to all the rings with radii from r=0 to R can be calculated by integration
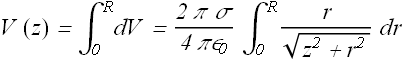
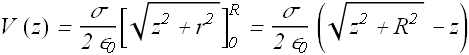
Calculating Field from the Potential
When a positive charge ![]() moves a distance
moves a distance ![]() in an electric field
in an electric field ![]() , the change in electric potential dV is given as
, the change in electric potential dV is given as
![]()
If we know the value of electric potential at each point, the electric field as per above equation will be
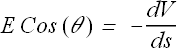
E Cos(θ) is the component of electric field along the displacement vector ![]() .
.
When we take derivative of electric potential with respect to a displacement vector ![]() , we get component of electric field along that displacement vector
, we get component of electric field along that displacement vector ![]() .
.
We can conclude that at any given point x, y and z components of an electric field can be computed as
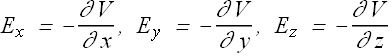
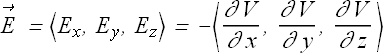
Electric Potential Energy of a System of Point Charges
Electric potential energy exists only for a system with two or more charged particles.
Therefore for a single charge particle system, the electric potential energy is zero.
Add other charges (Alt Click) and see how the potential energy of the system changes?
Electric potential energy U of a the system of point charges is the sum of electric potential energy of all the charge pairs present in the system. Each pair should be counted once.
Potential energy ![]() of each pair of charge is
of each pair of charge is
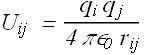
Example :
Total energy of a three charged particle system will be
![]()
Potential of a Charged isolated Conductor
A charged conductor is an equipotential surface:
Consider a charged conductor of arbitrary shape.
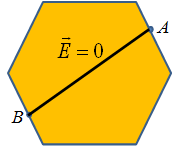
Let us move a charge from point A to point B, inside the conductor, the change in electric potential is given as
![]()
Electric field ![]() inside a conductor is zero, therefore
inside a conductor is zero, therefore
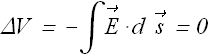
This shows that the electric potential at point A is equal to electric potential at point B.
In other words, a charged conductor surface is an equipotential surface.
Any charged conductor is an equipotential surface.
Electric potential inside a charges conductor is a constant :
Now consider a point B inside a charged conductor and point A on its surface.
The electric potential difference between point A and point B will be
![]()
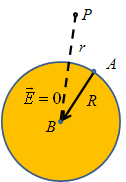 |
 |
 |
This shows that the potential at point A is equal to electric potential at point B.
Electric potential inside a charged conductor is constant.
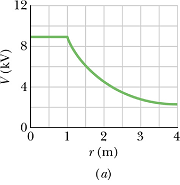
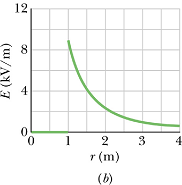
Electric potential outside a charged conductor at position r > R is
![]()
Inside the conductor electric potential is same as its value on the surface
![]()
Isolated conductor inside an electric field :
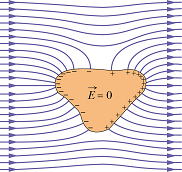
Surface of a charged conductor is an equipotential surface.
Electric field is always normal to an equipotential surface. Therefore
Electric field is always normal to the conductor surface.
The charge redistribute itself to make electric field inside the conductor zero.
Magnitude of electric field close to outside surface of the conductor is
![]()
