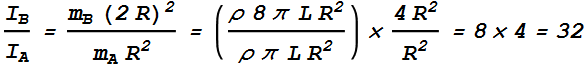Rotation

Objectives

In this chapter we will study the rotational motion of rigid bodies about a fixed axis.  
After finishing this chapter we should know following topics:

Angular displacement

Average and instantaneous angular velocity (symbol: ω).

Average and instantaneous angular acceleration (symbol: α)

Which angular quantities are vector?

Equations of motion for constant angular acceleration.

Relation between angular and linear quantities.

How to calculate the kinetic energy associated with rotation.

Rotational inertia also known as moment of inertia (symbol  I)

How to compute rotational Inertia of simple objects.

Parallel-Axis Theorem.

How to compute rotational Inertia of continuous object.

Rotation of a rigid body

What is a rigid body?

An object whose shape stays same as it moves is called a rigid body.

An ideal rigid body is non-existent.

An object in which the atomic forces are so strong that the little force needed to move it do not bend it, can be considered a rigid body.

Rotation

Following is an example of pure rotation (angular motion) of a rigid body.

We can see that every point of the rigid body moves in a circle whose center lies on a fixed axis (z-axis in this case).

This fixed axis is called the axis of rotation or the rotation axis.

Every point moves through the same angle during a particular time interval.

Rotational Variables: Angular Position

Consider a rigid body capable of rotating around z-axis.

Draw a reference plane (light pink) passing through the rotating axis and fixed in the rotating body.

View it from the top (projection on xy-plane), the reference plane looks like a reference line (dotted yellow).

Rotate the rigid body and watch the reference line.

It is perpendicular to the rotation axis and rotates with the body.

Presently it is making an angle θ with x axis.

θ is called the angular position of the rotating rigid body.

How θ is defined?

If s is the distance covered (blue arc) by the sphere and r is the radius of its circle, θ is defined as

In rotation, θ is always measured in radians (rad) rather than in revolutions (rev) or degrees.

In rotation, we do not reset θ to zero after each complete rotation.

θ for one complete rotation is

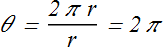
When the rigid body completes n rotations, its angular position will be

Rotational Variables: Angular Displacement

Rotate the rigid body from its present (initial) angular position to a different (final) angular position .

We can say that rigid body undergoes an angular displacement Δθ given by

At a given time if Δθ is the angular displacement of the rigid body, then Δθ is also the angular displacement of every particle within that body.

The angular displacement Δθ of a rotating body is either positive or negative:

Angular displacement in the counterclockwise direction is positive

Angular displacement in the clockwise direction is negative

Rotational Variables: Angular Velocity (ω)

Suppose that our rotating body is at angular position at time and at angular position at time .

We define the average angular velocity of the body in the time interval Δt from to .

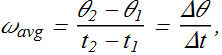
The (instantaneous) angular velocity ω, with which we shall be most concerned, is the limit of the ratio, as Δt approaches zero. Thus,

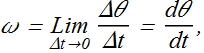
Rotational Variables: Angular Acceleration (α)

Let and be its angular velocities at time and time .

The average angular acceleration of the rotating body in the interval from to is defined as

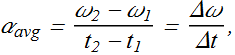
The (instantaneous) angular acceleration α, is defined as,

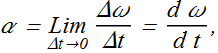
Problem 1(Rotational variables):

If a wheel is turning at 3.0 rad/s, How much time it takes to complete one revolution?

What is the total angle to complete one revolution?

How much time the wheel will take to complete this angle?

Problem 2(Rotational variables):

What is the angular speed of minute hand of a watch?

What is the total angle to complete one revolution in a watch?

How much time the minute hand of a watch will take to complete this angle?

Problem 3(Rotational variables):

A flywheel rotating at 12 rev/s is brought to rest in 6.0 s.
What is the magnitude of the average angular acceleration in of the wheel during this process?

What is the initial angular velocity of the fly wheel in rad/s?

What is the final angular velocity of the fly wheel in rad/s?

Are Angular Quantities Vectors?

The angular velocity     is a vector and points along the axis of rotation.

It is always perpendicular to the plane of rotation.

Anticlockwise rotation is considered as positive.

Clockwise rotation is considered as negative.

The direction of angular vectors   can also be established by using a right-hand rule, as shown:

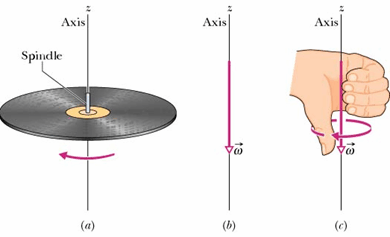
Curl your right hand about the rotating record, your fingers pointing in the direction of rotation. Your extended thumb will then point in the direction of the angular velocity vector.

Angular Acceleration

The angular acceleration   is a vector and points along the axis of rotation.

When angular acceleration points in the direction of angular velocity , it increases the angular velocity.

When angular acceleration points opposite to the direction of angular velocity , it decreases the angular velocity.

Watch following simulation with in opposite direction to initial .

What about angular displacement?

Angular displacements θ (unless they are very small) is not a vector.

Vector addition is always commutative

Let us consider two angular displacements

is π/2 anti-clockwise rotation along x axis

is π/2 anti-clockwise rotation along y axis

Simulation (a) represents

Simulation (b) represents

(a)	(b)

We can see that final result in (a) and (b) is not same, means

Angular displacements fail commutative test. Therefore angular displacement is not a vector.

Rotation with constant Angular Acceleration

Equations of Motion for Constant Linear Acceleration and for Constant Angular Acceleration

Equation No.	Linear Equation	Missing Variable		Angular Equation
1
2		v	ω
3		t	t
4		a	α
5

Relating the linear and Angular Variables

Linear Speed of rotating object

Consider an object rotating in a plane (x y-plane).

Distance covered s is related to angular displacement θ and radial position r.

Therefore linear speed v will be given as

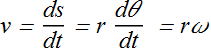
v is also the magnitude of tangential velocity

Linear acceleration

There are two kind of linear accelerations, associated with a rotating object.

Radial acceleration or centripetal acceleration (green arrow) .

Tangential acceleration (Yellow arrow) .

Radial acceleration or centripetal acceleration only changes the direction of the (tangential) velocity.

Tangential acceleration only changes the magnitude of the (tangential) velocity.

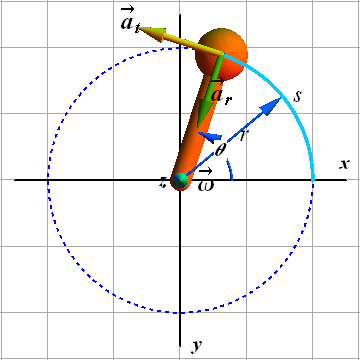
Radial acceleration or centripetal acceleration is related to the magnitude of tangential velocity v and radius r.

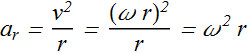
Tangential acceleration is the change in magnitude of tangential velocity v with time.

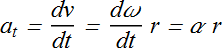
α is the magnitude of angular acceleration.

Checkpoint-1: (Relating linear and Angular variables)

A wheel starts from rest and spins with a constant angular acceleration.
As time goes on how the magnitude and direction of the linear acceleration vector change?

Hints : Total linear Acceleration

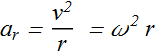
Kinetic Energy of Rotation

Observe the rotation of two identical spheres in a plane.

Both the spheres have identical mass m and are attached with a mass less rod.

Both the spheres are rotating with same angular velocity     .

What is the kinetic energy of particle A and B?

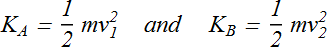
Is ?  

Total kinetic energy of this system will be

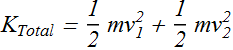
In terms of angular velocity

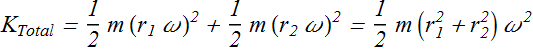
Term is called rotational inertia or moment of inertia of this two spheres system about its axis of rotation.

Symbol of rotational inertia is I and kinetic energy of two sphere system can be written as

Checkpoint-2: (Kinetic energy of rotation)

Three identical balls are tied by light strings to the same rod and rotate around it, as shown below.
(a) Rank the balls according to their kinetic energy, least to greatest.
(b) Rank the balls according to their rotational inertia, least to greatest.

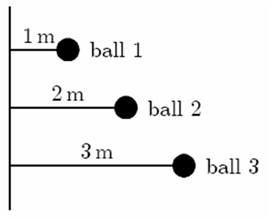
Hint : All the balls have same angular velocity.

Kinetic Energy of a rotating system with n particles.

By adding kinetic energy of all the particles of a rotating system we can obtain the kinetic energy of the system as a whole.

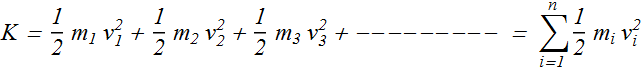
is the mass of the ith particle and is its speed.

Since angular velocity ω of all the particles is same, therefore we can use the relation

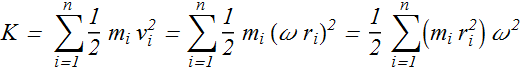
is the minimum distance of the ith particle from the axis of rotation.

The rotational inertia (or moment of inertia) I of a n particle system with respect to the axis of rotation is defined as

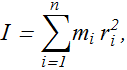
Therefore, kinetic energy K about the rotation axis is given as

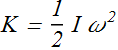
Rotational inertia is always computed about a given rotation axis, if rotation axis change the rotational inertia of the system will change.

If position of particle changes with respect to axis of rotation, the rotational inertia of the system will change.

Checkpoint-3: (Rotational Inertia)

If the position of sphere moves closer to axis of rotation, (a) will the rotational inertia increase, decrease or remain same?

Hint :

Calculating the Rotational Inertia

Example - 1

Let us compute rotational inertia of a two sphere system rotating about a rotation axis passing through center of mass (com).

Rotational Inertia for such a system about an axis through the center of mass will be computed as

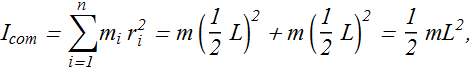
It is assumed that connecting rod of length L is of negligible mass.

Example-2

Let us compute rotational inertia of same two sphere system, when it rotates around an axis passing through center of one of the sphere?

Rotational Inertia I for such a system about an axis passing through center of one of the sphere will be computed as

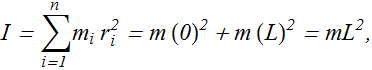
It is assumed that connecting rod of length L is of negligible mass.

Parallel-Axis Theorem

If the rotation axis shifts with respect to the center of mass, will the rotational inertia change?

If is the rotational inertia about an axis through its center of mass, then rotational inertia I about any other axis parallel to this axis is given as

Here M is total mass and h is the perpendicular distance between the given axis and the axis through the center of mass.

This equation is known as the parallel-axis theorem.

The rotational inertia of the two particle (sphere) system about an axis through the left particle can be found with the help of this theorem.

for two particle with L distance apart is  

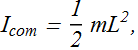
I about any other axes parallel to the axis passing through the center mass will be  

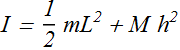
If h=L/2, then

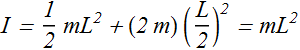
It is the same value as we obtained for such a system in Example-2.  

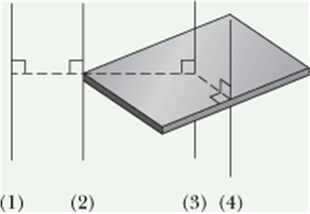
Checkpoint-4: (Parallel axis theorem)

The figure shows a book-like object (one side is longer than the other) and four choices of rotation axes, all perpendicular to the face of the object.
Rank the choices according to the rotational inertia of the object about the axis, greatest first.

Rotational Inertia of continuous object

If a rigid body consists of a great many adjacent particles (it is continuous), above Equation would require a computer.

We can replace the sum with an integral and define the rotational inertia of the body as

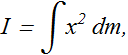
Consider a uniform rod of mass M and length L, on an x axis with the origin at the rod's center, the rotational inertia of the rod about the perpendicular rotation axis through the center  can be computed by integral method.

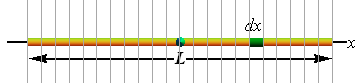
For a uniform rod, the ratio of mass to length is the same for all the elements and for the rod as a whole. Thus,

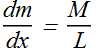
It can be rewritten as

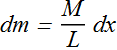
The Rotational Inertia of the rod can be computed as

Problem 6: (Rotational Inertia)

What is the rotational inertia of a thin cylindrical shell of mass M, radius R, and length L about its central axis (X, X’)?

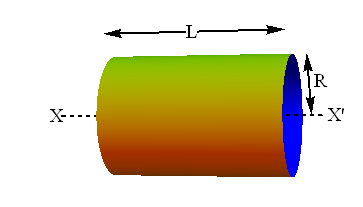
Hint : All the particles of the cylinder are equidistant from the rotating axis.

Solution :

Some Rotational Inertia

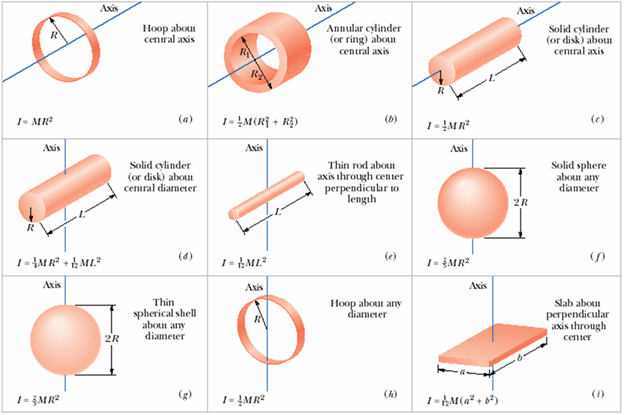
Problem-7 (Rotational Inertia):

A and B are two solid cylinders made of aluminum. Their dimensions are shown. What is the ratio of the rotational inertia of B to that of A about the common axis (X, X’)?

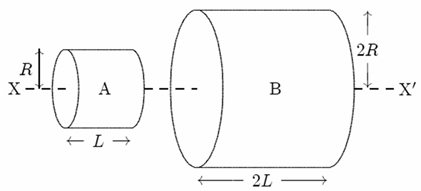
Hint: The Rotational inertia of a solid cylinder along its axis is

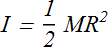
Solution :

Let us consider ρ is the density of Aluminum, mass of a cylinder will be

Masses of two cylinders are